<<< interlibrary.narod.ru

Памяти Стефана Маринова

      Используя многочисленные группы наблюдательных данных, (однородные в пределах каждой такой группы), можно получить не менее 10000 эмпирических зависимостей вида Z-N, Z-θ, m-Z, S-Z, S-N, m-N, S-θ, m-θ, θ-N (где S, m – плотности потока и звездные величины в разных полосах в диапазоне от радиоволн до гамма-квантов, θ – угловые размеры, Z – красное смещение, N  - наблюдаемое число объектов), пргодных для тестирования любой достаточно разработанной космологической теории.

Хорошо известны принципиальные различия между такими использемыми в  космологии концепциями как классическая [ 1 ], фрактальная [ 2 ], релятивистская [ 3 ], квантовая [ 4 ]. Здесь я остановлюсь на некоторых удивительных чертах сходства между ними.

1. Классическая система мира и система единого поля

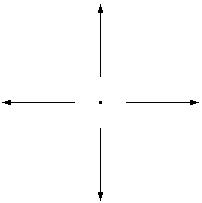
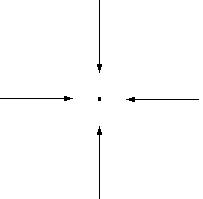
Основой любой космологии являются открытые в рамках классической системы мира закон Кеплера для освещенности и закон всемирного тяготения Ньютона [ 1 ] (см. рис.1):

Рис.1. Закон Кеплера и закон Ньютона по существу описывают встречно направленные и взаимно дополняющие процессы.

где: G –  постоянная Ньютона,  L, M – светимость и масса объекта, S_bol, g – полная плотность потока энергии электромагнитного излучения и ускорение на расстоянии r. Связь между звездными величинами и плтностями потока дается формулой Погсона

m=-2.5 lgS + C.

где плотность потока в Янских; при этом С = 8.185 для полосы U. C = 9.118 для полосы B и так далее.

В рамках любой системы мира закон Кеплера используется для определения расстояний астрономическими методами, а закон Ньютона при динамических расчетах космических систем. Поразительная аналогия между этими основополагающими законами позволяет предположить, что второй из них связан с «втеканием» энергии физического вакуума в любой объект, обладающий массой покоя, в то время как первый характеризует расход энерегии в виде излучения. На большой пространственно-временной шкале расход должен равняться приходу. На малой шкале необходимо учитывать, что энерговыделяющие  ядерные реакции приводят к тому, что, к примеру, Солнце излучает в 25 раз больше энергии, чем получает из физического вакуума в виде П-фотонов (продольных фотонов де Бройля), а энергопоглощающие ядерные реакции приводят  к тому, что Земля поглощает в 2 миллиона раз больше, Нептун  в 200 тысяч, Сатурн в 100 тысяч, Юпитер в 30 тысяч раз больше, чем эти тела отдают в космическое пространство в виде «внутреннего тепла» [ 4 ]. Другой интересный результат можно получить на основе исследования уравнения (1), смотрите в следующем разделе, впервые предложенного Нейманом, затем Зелигером в рамках классической системы мира.

2. Релятивистская система мира и система единого поля

Стандартная релятивистская космология основана на решениях космогологического уравнения Эйнштейна

где P = R/c – космологический масштабный фактор, k – кривизна пространства, принимающая значения +1, 0 или –1; ρ_ср(t) – зависимость средней плотности вещества от времени t; R – радиус гравитационного взаимодействия, равный радиусу Метагалактики; с – скорость света.

Решения этого уравнения либо близкого к нему, содержащего космологический лямбда-член, при условии ρ_срP³ = Constant, позволяют выполнять космологическое тестирование на основе определения свободных параметров, соответствующих разным группам наблюдательных данных. В случае k = -1 такое решение удобно представить в параметричекском виде с применением экспонент, гиперболического синуса для P, косинуса для t  и тангенса для скорости расширения Вселенной [ 3 ].

В теории единого поля используется представление о  том, что движущийся в свободном пространстве микрообъект на каждом отрезке, равном длине волны де Бройля, λ = h/p, теряет энергию h Н, равную энергии П-фотона, где p – импульс, h, H – постоянные Планка и Хаббла. Отсюда, используя соотношение для энергии фотона или нейтрино E = pc, можно получить дифференциальное уравнение

решение которого дает экспоненциальные зависимости

и, соответственно, логарифмическую зависимость расстояния от красного смещения

r=Rln(1+Z).

Но если микрообъект обладает массой покоя m₀, тогда вместо E=pc необходимо воспользоваться более общим соотношением

При этом нетрудно получить соотношения для энергии E частицы, ее испульса p и скорости v, содержащие гиперболические функции и экспоненты

,

,

.

Эти же результаты для микрочастиц разного типа можно  получить на основе не только квантовых, но и классических представлений, если тщательно рассмотреть все возможные решения уравнения Пуассона для гравитационного потенциала Ψ

,

приняв следующее:

1. ,

2.  Микрообъект движется в свободном пространстве, где ρ=0.

3.  Микрообъект движется по прямой, откуда следует целесообразность рассмотрения уравнения Пуассона, записанного не в сферических, а в декартовых координатах.

4.  Наконец, описание энергетического взаимодействия микрообъекта с «общим гравитационным полем» должно не зависеть от направления его движения, т.е.

,   

Итак, мы имеем разнообразные космологические модели, две из которых описываются с использованием экспонент и гиперболических функций (табл.1)

Таблица 1.

Сходство и различие космологических моделей

В обеих моделях масса Вселенной – бесконечная величина. В математическом и даже в физическом отношении модели близки, поскольку импульс –вектор, т.е. пространствоподобная величина, энергия – скаляр, т.е. времяподобная величина. Поэтому тот, кто не владеет методами космологического тестирования, может ошибиться… в бесконечное число раз.

3. Фрактальная система мира и система единого поля

Согласно фрактальной системе мира [ 2 ], зависимость числа объектов N от  расстояния r должна иметь вид:

где D – играющая здесь роль свободного параметра фрактальная размерность, которая может принимать значения 3, 2 или 1.

Но если под N  понимать наблюдаемое число объектов, то случаи D=2 и 1 могут быть объяснены не неоднородным распределением объектов в крупных пространственных масштабах, а совместным влиянием ряда других факторов [ 4 ] и в первую очередь направленностью излучения активных объектов, характеризуемых, как установлено И.С.Шкловским, синхротронными спектрами излучения, а также направленностью излучения «космических лазеров». При этом зависимости произведений S_bol·N от r или  от Z для разных типов излучателей должны быть одинаковыми (табл. 2), а сами эти произведения должны характеризовать среднюю мощность, излучаемую объектами данного типа в фиксированном объеме.

Таблица 2.

Исходные соотношения в функции расстояния.

Используя исходные соотношения в функции расстояния или красного смещения, можно найти другие зависимости для основных классов внегалактических объектов и даже для далеких внегалактических лазеров, которые пока остаются гипотетическим классом объектов. Разумеется, конкретные соотношения должны учитывать наблюдательные эффекты селекции и содержать те или иные астрофизические поправки. Наличие в выражениях для плотностей потока, объемной  плотности энергии и гравитационного потенциала затухающей экспоненты показывает, что данная теория не отягчена фотометрическим, термодинамическим и гравитационным парадоксами. В частности интегрирование по бесконечному объему  не приводит к бесконечным значениям плотности энергии, потенциала, ускорения  и других величин. Еще одной особенностью является то, что для каждого типа излучателей (табл.2) теория единого поля дает однозначные зависимости, не содержащие параметров типа  k  или D. Тестировать эту теорию просто. Не ключ ли это к надписям  на Розетском камне? Надписям, горящим а безднах пространства и времени. Надписях на трех  языках:

ЛИТЕРАТУРА

1.      Ньютон Исаак. Математические начала натуральной философии. М. 1989.

2. Charlier C.V.L. Arkiv for Mat., Astron. och Fys. 1908. 4.P.1.
3. Ландау Л.Д., Лифшиц Е.М. Теория поля.М.Наука. 1967. стр. 440.
4. www.interlibrary.narod.ru (Astronomy Ns 59 –68, Physics Ns 1, 5, Biology Ns 33,26).