Р а з д е л I
О методике генетического анализа
механических параметров вращения производных звездной эволюции
Данный анализ не претендует на
абсолютную точность полученных цифр, но его цель — показать генетическую
связь механических параметров небесных тел, образовавшихся из выброшенных
двумя тесными звездами оболочек и прошедших стадию планетарных туманностей, и
восстановить по ней основную канву процесса эволюции Солнечной системы [7].
Отрыв оболочек от звезды
происходит вследствие смены режимов атомообразования под действием скачка
нейтринного давления в зоне звездной трансформации, под наружной оболочкой
светила, где возникают радиально направленные от его центра силы, действующие
на элементы массы оболочки [8]. Выносящие оболочку наружу нейтринные потоки
оказываются интенсивнее притекающих к звезде эфирных потоков, создающих силы
тяготения.
Сила отрыва оболочки от
«новой» звезды по Соболеву В. В. [2] должна быть не менее силы притяжения по
Ньютону оболочки массой m к оставшейся части звездной массы M
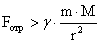 , ,
где r — радиус звезды после потери
оболочки,
g — гравитационная постоянная 6, 67×10–8 см3/г×с2.
Из выражения для импульса силы
отрыва оболочки можно определить нижний предел скорости Vr выброса
вещества звезды во время сброса оболочки
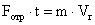 , ,
откуда
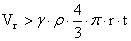 , (*) , (*)
где r — плотность субстанции звезды,
t — продолжительность развития
деформации взрыва.
Далее заметим, что полюсные
области оболочки звезды после отрыва движутся параллельно оси ее вращения, не
сохраняя вращательного момента светила, так как их моменты инерции
пренебрежимо малы. Движение полюсных частей оболочки здесь рассматривать не
будем.
Экваториальная часть оболочки,
опоясывающая звезду как кольцо, должна при выбросе одинаковой силы взрыва по
периметру сохранить свою кольцеобразную, вернее, тороидальную форму. При этом
благодаря центральному характеру действующих сил отрыва траектории фрагментов
экваториальной части оболочки должны быть плоскими кривыми линиями,
расположенными в экваториальной плоскости звезды, как проходящей через центр
действия сил. Вращающаяся звезда при сбросе оболочки сообщает ей определенный
импульс вращения (момент количества движения), который при отсутствии
последующих прямых воздействий остается характеристикой, обуславливающей
вполне определенные параметры вращательного движения формирующегося спутника
как производного ее эволюции: размер орбиты и угловую скорость w. Импульс вращения L небесного тела, как часть импульса вращения родительской
звезды, может изменяться лишь при непосредственном контакте с другим телом,
например, в столкновении, в котором осуществляется перераспределение импульса
вращения.
Инерционность вращающегося
тела оценивается его моментом инерции I, зависящим помимо массы тела еще от
квадрата его радиуса инерции.
Итак, элемент m массы звезды в ее экваториальной
части под действием силы отрыва отбрасывается на некоторое расстояние от оси
вращения звезды r > rзв и одновременно поворачивается в
плоскости выброса на некоторый угол j (рис. I).

Рис.
1. Движение выброшенного единичного элемента массы
в полярных координатах (r; j) в экваториальной плоскости звезды.:
Vj
= w´r, Fj
= 2w´Vr, Fr = – w2r
При изучении движения
сброшенной звездой оболочки рекомендуется одновременно учитывать и возможное
дальнейшее ускорение оболочки выбрасываемым из звезды веществом и торможение
ее межзвездной средой, снижение ее скорости и в некоторых случаях деформацию
[2]. Если оболочка выбрасывается внутри пылевой туманности, то ее торможение
особенно существенно [2].
Основное торможение оболочка
получает от возникшей силы инерции — реакции на первоначальное ускорение.
После исчерпания внутреннего
нейтринного давления зоны звездной трансформации элемент сброшенной оболочки
начинает двигаться по инерции, испытывая торможение от притекающих к звезде
эфирных потоков, одновременно гравитационно удерживающих его около звезды. На
единицу массы оболочки с приобретением ею радиальной скорости Vr действуют следующие силы инерции: в радиальном
направлении — 1 – центробежная Fцб, 2 – кориолисова сила 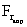 , связанная с окружной скоростью Vj и направленная против центробежной; в окружном
направлении — 3 – кориолисова сила Fj, связанная с радиальной скоростью Vr, уменьшающаяся вместе с ней до нуля и направленная
в сторону окружной скорости. Радиальное торможение гравитационной природы
из-за перевеса притекающих эфирных потоков над заслоняемыми звездой [9]: , связанная с окружной скоростью Vj и направленная против центробежной; в окружном
направлении — 3 – кориолисова сила Fj, связанная с радиальной скоростью Vr, уменьшающаяся вместе с ней до нуля и направленная
в сторону окружной скорости. Радиальное торможение гравитационной природы
из-за перевеса притекающих эфирных потоков над заслоняемыми звездой [9]:
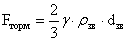 , ,
где rзв и dзв —
плотность вещества и диаметр звезды.
Радиальная и окружная
плотности сил инерции — тормозящей Fr и поворотной Fj:
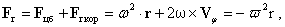 (1) (1)
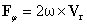 . (2) . (2)
Благодаря замедлению,
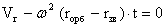 , (2a) , (2a)
прекращается
радиальное движение элементов оболочки на радиальной координате rорб (радиусе
орбиты), где Vr = 0. Уравнение (2а) показывает, что rорб
зависит от начальной скорости выброса, размера звезды и угловой скорости ее
вращения перед выбросом.
Для самой звезды потеря ею
оболочки проходит не бесследно: у нее уменьшается ее собственный момент
инерции как за счет потери массы, так и за счет уменьшения радиуса инерции.
На каждой стадии развития
звезды, завершающейся сбросом очередной оболочки, материальная система —
звезда с одними параметрами (радиусом сферы, плотностью субстанции, массой,
угловой скоростью вращения) преобразуется в новую материальную систему:
звезду с другими параметрами и сброшенную оболочку, Элементы последней,
преобразуясь в планетное тело или кольцо разрозненных астероидов, остаются
генетически связанными с параметрами родительской звезды в момент (до) сброса
данной оболочки. Эта генетическая связь не подвергается изменениям из-за
сброса звездой последующих оболочек.
Действительно, согласно закону
сохранения момента количества движения [4] производная по времени от импульса
вращения материальной системы относительно какой-нибудь неподвижной точки
равна общему моменту всех сил относительно той же точки, действующих на
материальную систему:
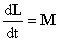 , или , или 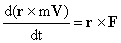 . (3) . (3)
Исходная материальная система
— звезда, которая должна сбросить оболочку, подвергается воздействию
центральных сил ее отрыва, которые не имеют момента относительно неподвижной
точки — центра массы звезды. В то же время с наступившим выбросом наружного
слоя по всей сферической поверхности и равномерным уменьшением радиуса сферы
центр массы звезды должен оставаться на своем месте, что исключает
возникновение дополнительных вращающих моментов сил.
Тогда для рассматриваемой
звезды
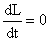
и L = const.
Постоянство импульса вращения требует, чтобы L звезды до сброса оболочки без потерь преобразовался
в импульс вращения новой системы.
Покажем, что угловая скорость
вращения w элемента массы сброшенной оболочки есть его
генетическая характеристика, сохраняющая угловую скорость вращения звезды до
выброса.
Для этого проанализируем
действующие на единичный элемент массы сброшенной оболочки силы инерции Fr и Fj по
уравнениям (1) и (2). Все силы инерции Fr являются центральными силами, т. к. проходят через
неподвижную точку — центр массы звезды. За счет них не может происходить
изменение импульса вращения движущегося элемента массы сброшенной оболочки.
Импульс вращения L движущейся массы m изменяется
за счет действия кориолисовой силы инерции Fj , имеющей момент M = r ´ Fj = r
´ 2w
´ Vr × m относительно неподвижной точки. После определения
левой части уравнения (3) для движущейся массы m:
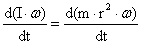
и в
результате ее преобразования получено уравнение
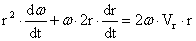 . .
Его решение путем преобразования
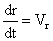
дает окончательное выражение
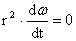 , ,
из
которого следует, что w = const есть
неизменная величина на пути следования элемента массы сброшенной оболочки,
остающаяся в размерах, приобретенных от звезды в момент данного выброса.
Определим импульс вращения
звезды до сброса оболочки:
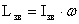 , (4) , (4)
где
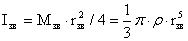 . .
Определим импульс вращения
новой системы:
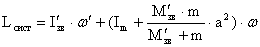 , (5) , (5)
где 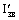 и и 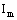 — моменты инерции
относительно параллельных осей, проходящих через центры масс «новой» звезды и
элемента m массы сброшенной оболочки, которая не только вращается вокруг
внешней оси, но и поворачивается вокруг своей оси с радиусом инерции г/2 (как
до выброса, так и после него): — моменты инерции
относительно параллельных осей, проходящих через центры масс «новой» звезды и
элемента m массы сброшенной оболочки, которая не только вращается вокруг
внешней оси, но и поворачивается вокруг своей оси с радиусом инерции г/2 (как
до выброса, так и после него):
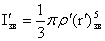
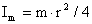 . .
Второе слагаемое в скобках —
момент инерции общего тела относительно новой параллельной оси, проходящей
через их общий центр масс, где а — расстояние между полярными осями центров
двух масс 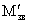 и m [4]. и m [4].
Параметры обеих звезд
Юпитер—Солнце на каждой стадии развития после сброса каждой оболочки
определяются из уравнения
Lзв = Lсист .
(6)
При оценке порядка величин
членов уравнения (5) оказывается, что второе слагаемое имеет пренебрежимый
порядок малости, а учет его третьего слагаемого при решении уравнения (6)
обеспечивает бóльшую точность, чем при отсутствии его учета, — в
пределах 1 ÷ 5%. Практические вычисления по решению уравнения (6)
выполнены как с учетом третьего слагаемого (5), так и без него (для
сравнения).
Расчет по приведенной методике
при rЮ = 1,33
и r¤ = 1,4 г/см3 не учитывает изменения
плотности вещества звезды в процессе эволюции, так как не имеется достаточно
достоверных сведений об этом изменении, хотя из косвенных соображений
следует, что rзв в
процессе эволюции должна расти: плотность вещества ее производных, а
следовательно сброшенных оболочек последовательно растет: у Юпитера от 1,7 до
5,52 г/см3, у Солнца от 2,20 до 5,30 г/см3. Величина гравитационной
постоянной так же принимается не изменяющейся во времени, хотя это и не
бесспорно.
Р а з д е л 2
Юпитер со своими производными
Расчет ведется назад во
времени, от 7-й к 1-й производной.
7-я производная — Амальтея.
Угловая скорость обращения w7 = 2p рад/(11 ч 57 мин) есть угловая скорость вращения
Юпитера до сброса 7-й оболочки. Угловая скорость вращения Юпитера после
сброса 7-й оболочки составляет 2p рад/(9 ч 50 мин). С учетом а7 = 2,5rЮ решено
уравнение (6) для 7-й стадии развития Юпитера.
Его решение как с учетом
последнего слагаемого, так и без него, дает размер Юпитера перед сбросом 7-й
оболочки
rю6 = 1,04 rю7 = 0,74 × 1010 см.
Масса Юпитера до сброса 7-й
оболочки или после сброса 6-й оболочки
Mю6 = 1,125 MЮ ,
где МЮ — современная масса Юпитера.
6-я производная — Земля.
Угловая скорость ее
собственного вращения 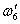 претерпела изменение
по сравнению с генетической претерпела изменение
по сравнению с генетической 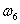 из-за столкновения
Земли с Луной и приобретения наклона к первоначальной оси вращения,
параллельной оси вращения Юпитера [7]. Радиус обращения Земли вокруг Юпитера
найден как для кеплеровской орбиты при генетической угловой скорости из-за столкновения
Земли с Луной и приобретения наклона к первоначальной оси вращения,
параллельной оси вращения Юпитера [7]. Радиус обращения Земли вокруг Юпитера
найден как для кеплеровской орбиты при генетической угловой скорости 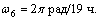 обращения a6 = 2,5 × 1010 см = 3,5 rЮ. обращения a6 = 2,5 × 1010 см = 3,5 rЮ.
Уравнение (6) для 6-й стадии
развития Юпитера после его решения дает размер Юпитера перед сбросом 6-й
оболочки
rю5 = 1,145 rю = 0,815 × 1010 см,
а без
учета последнего слагаемого rю5 = 1,141 rю .
Масса Юпитера до сброса 6-й
или после сброса 5-й оболочки:
Mю5 = 1,5 MЮ .
По упрощенному варианту Mю5 =
1,485 MЮ .
5-я производная — Марс.
Угловая скорость вращения
Марса w = 2p /24,6 рад/ч могла отклониться от генетической в
момент изменения угла наклона экватора до 25° к плоскости его орбиты [6] (из-за столкновения со
2-й производной Солнца [7]).
Поскольку Земля и Марс должны были возникнуть в
экваториальной плоскости Юпитера, экватор которого наклонен к плоскости его
орбиты на »3°, то изменение угла наклона марсианской оси вращения
от первоначальной осуществлялось в пределах a = 25 – 3 = 22° или 0,38 радиан, так что первоначальная 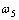 могла составлять могла составлять
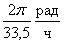 . .
Кеплеровской орбитой для
генетической w5 = 2p/33,5 рад/ч
является радиус обращения а = 3,6 × 1010 см = 5 rЮ . Уравнение (6) для 5-й стадии развития Юпитера
после точного решения дает
rю4 = 1,282rЮ =
0,912 × 1010 см.
Масса Юпитера до сброса 5-й
или после сброса 4-й оболочки по приближенной оценке
Mю4 = 1,4Mю5 = 2 MЮ ,
по более точной оценке Mю4 = 2,1
MЮ .
4-я производная — Ио.
Параметры обращения Ио
составляют a = 4,22 × 1010 см и w = 2p/42,5 рад/ч .
Уравнение (6) для 4-й стадии
развития Юпитера после его точного решения дает размер Юпитера перед сбросом
4-й оболочки rю3 = 1,345rЮ =
0,957 × 1010 см, приближенно rю3 =
0,939 × 1010 см.
Масса Юпитера до сброса 4-й
или после сброса 3-й оболочки по приближенной оценке Mю3 =
1,15Mю4 = 2,3
MЮ ,
более точно Mю3 = 2,43 MЮ .
3-я производная — Европа.
Параметры обращения Европы
составляют а = 6,7 × 1010 см и w = 2p/85,2 рад/ч .
Из уравнения (6) для 3-й
стадии развития Юпитера следует, что rю2 =
1,545 × rЮ = 1,1 × 1010 см, приближенная оценка дает rю2 =
1,08 × 1010 см.
Масса Юпитера до сброса 3-й
или после сброса 2-й оболочки соответственно Mю2 =
3,68MЮ и менее точно Mю2 =
3,5 MЮ .
2-я производная — Ганимед.
Параметры обращения Ганимеда
составляют
а = 10,71 × 1010 см
и
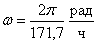 . .
Из уравнения (6) для 2-й
стадии развития Юпитера следует, что rю1 =
1,78 × rЮ = 1,26 × 1010 см, приближенная оценка дает rю1 =
1,24 × 1010 см.
Масса Юпитера до сброса 2-й
или после сброса 1-й оболочки соответственно Mю1 =
5,64MЮ и менее точно Mю1 =
5,32 MЮ .
1-я производная — Каллисто.
Параметры обращения Каллисто
составляют
а = 18,8 × 1010 см
и
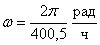 . .
Из уравнения (6) для 1-й
стадии развития Юпитера следует, что rю0 =
2,11 × rЮ = 1,5 × 1010 см, приближенная оценка дает rю0 =
2,10 rЮ = 1,47 × 1010 см.
Масса Юпитера до сброса 1-й
оболочки составляла по более точной оценке Mю0 =
9,39MЮ и менее точно Mю0 =
9,26 MЮ .
Р а з д е л 3
Солнце со своими производными
Расчет следует проводить назад
во времени, от 7-й к 1-й производной. Однако среди 7-ми солнечных производных
по 4-м сброшенным оболочкам нет достаточно достоверных сведений об их
механических параметрах вращательного движения. В том числе по еще не
проявившей себя 7-й производной — Вулкану по Леверье, оказывающему возмущения
орбитальному движению Меркурия, 4-й сброшенной оболочке — кольцу
металлических астероидов, 2-й сброшенной оболочке — кольцу углистых
астероидов и 2-й планете Солнца и, наконец, 1-й оболочке — водородно-гелиевой
производной с неизвестной судьбой. В этой связи достоверность выполненных
расчетов должна проверяться определением точек Лагранжа двух звезд Юпитера и
Солнца в ходе эволюции двойной системы, местоположение которых ограничивает
область действия притяжения каждой из двух звезд, а неустойчивость баланса
сил служит причиной столкновения конкурентов на пересекающихся орбитах
производных двух звезд, особенно при перестройках системы.
В решении уравнения (6) для
развития Солнца роль последнего члена (5) становится пренебрежимо мала, так
как массы его производных пренебрежимо малы в сравнении с MС .
7-я производная — от синтеза 5-го периода элементов
Поскольку параметры оболочки,
сброшенной Солнцем в наименее отдаленное от нас время (227 млн. лет тому
назад) еще неизвестны, то по аналогии убывания размеров орбит от 3-го к 4-му
солнечному периодам ориентировочный радиус орбиты рассматриваемой оболочки
можно принять 0,285 а.е. = 61,2 rС. Угловую скорость обращения оболочки определяем из
закона Кеплера при а7 =0,285 а.е. как
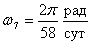 . .
Это
значение является ориентировочной скоростью обращения 7-й сброшенной Солнцем
оболочки, при сбросе которой Солнце потеряло массу и увеличило угловую
скорость вращения до
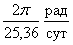 . .
Уравнение (6) для 7-й стадии
развития Солнца после его решения, как точного, так и приближенного дает размер
Солнца до сброса 7-й оболочки:
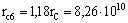 см. см.
Масса Солнца до сброса 7-й или
после сброса 6-й оболочки:
Mc6 = 1,64 MC.
6-я производная — Меркурий
Угловая скорость обращения
Меркурия
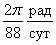 , ,
а большая полуось орбиты а6
= 0,38 а.е. = 81,7rC.
Уравнение (6) для 6-й стадии
развития Солнца после его решения дает для размера Солнца до сброса 6-й
оболочки:
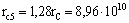 см. см.
Масса Солнца до сброса 6-й или
после сброса 5-й оболочки:
Mc5 = 2,097 MC.
5-я производная Венера — от синтеза 4-го периода
Угловая скорость обращения
Венеры
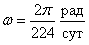 , ,
большая
полуось орбиты а5 = 0,72 а.е. = 154,8rC.
Уравнение (6) для 5-й стадии
развития Солнца после его решения дает размер Солнца до сброса 5-й оболочки:
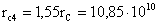 см. см.
Масса Солнца до сброса 5-й или
после сброса 4-й оболочки
Mc4 = 3,72 MC.
4-я сброшенная оболочка (М-астероидное кольцо)
Точные значения генетических
параметров обращения металлических астероидов получить затруднительно. Период
обращения металлических астероидов составляет в среднем величину w4 около
300 суток, чему соответствует кеплеровская орбита со средним радиусом обращения
0,87 а.е.
Убыстрение вращения Солнца в
результате сброса 4-й оболочки могло составить 300/224 = 1,339 раз. Из
уравнения для импульса вращения Солнца можно получить, что его размер перед
4-й вспышкой составлял
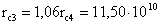 см. см.
Масса Солнца до сброса
четвертой или после сброса 3-й оболочки составляла
Mc3 = 1,19 Mc4 = 4,42
MC.
3-я сброшенная оболочка (кольцо S-астероидов и Луна)
от синтеза 3-го периода
Угловая скорость собственного
вращения силикатных астероидов трудно определима из-за малости их размеров, а
из сравнения
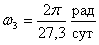
Луны с
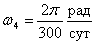
следует
сделать вывод о том, что после сброса 3-й оболочки момент инерции Солнца
резко увеличился в 300/27,3 = 11 раз. Это явление может означать поглощение
Солнцем чужеродной массы, увеличившей в итоге массу светила предположительно
в 1,623 = 4,25 раза.
Размер Солнца перед 3-й
вспышкой
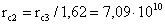 см, см,
т. е.
почти как современный, а масса Mс2 = 4,42/4,25 = 1,039 MC.
Импульс вращения или
количество вращения Луны в 3-й оболочке сразу после выброса оценивается
уравнением (5) из двух членов:
Lл = Lсобст. л
+ Lл–с ,
из
которых первый член имеет пренебрежимый порядок малости.
Количество вращения двойной
планеты Земля-Луна оценивается уравнением (5) из 5-ти членов:
Lз–л = Lсобст. з
+ Lсобст. л + Lобщ. з–л + Lс–з + Lс–л ,
из
которых определяющими оказываются два последних в сравнении с пренебрежимой малостью
остальных.
2-я сброшенная оболочка — кольцо С-астероидов с
осколками углеродистой планеты — от синтеза 2-го периода
Из второй сброшенной Солнцем
оболочки образовалась мощное кольцо углистых астероидов и 2-я планета,
разрушившаяся в столкновении с Марсом. Это показывает сопоставление их
импульсов вращения.
Момент
инерции и импульс вращения 2-й планеты
Солнца с неизвестной массой m2 выражены с ориентировкой на массу Луны через массу
Марса, заместившего 2-ю планету на ее орбите (rмар =
3,35 × 108 см, r2 = 1,7 × 108 см, rмар =
3,95 г/см3, r2 = 2,2
г/см3):
m2 = mмар/13,7.
Гипотетический импульс
вращения 2-й планеты, полученный ею от Солнца:
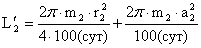 , ,
где первое
слагаемое можно опустить за его малостью, так же как и в импульсе вращения
Марса на орбите Юпитера, обращающихся вокруг протосолнца.
Убыстрение вращения Солнца во
время сброса 2-й оболочки:
100 сут/27 сут = 3,7 раза.
Перед сбросом 2-й оболочки Солнце
имело размер:
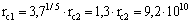 см. см.
Масса Солнца перед сбросом
второй и после выброса первой оболочки:
Mс1 = 2,19 × Mс2 =
2,27 × MC.
I-я сброшенная оболочка — от синтеза 1-го периода
Относительно I-й производной
Солнца — водородно-гелиевой планеты, кометы или разрозненных астероидов не
известны ни масса, ни характер обращения.
Если принять гипотетическую
угловую скорость вращения Солнца до сброса I-й оболочки
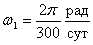 , ,
то
увеличение его угловой скорости вращения во время I-й вспышки составило
300/100 = 3 раза. Из уравнения для импульса вращения Солнца можно получить
его гипотетический размер до выброса I-й оболочки:
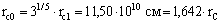 . .
А первоначальная масса могла
составлять
Mс0 = 1,95 × Mс1 =
4,43 × MC.
Р а з д е л 4
О возможных перемещениях точек Лагранжа в процессе
развития двойной звезды Юпитер—Солнце
Для системы двух обращающихся
одно относительно другого небесных тел существуют 4 точки Лагранжа [3], две
из которых лежат на прямой, соединяющей тела.
Перемещение точек Лагранжа в
тесной системе Юпитер—Солнце должны были неизбежно происходить в связи с
изменением соотношения масс звезд. Соотношение масс компонент MЮ/MС
менялось скачкообразно в следующих значениях: от 2,1 × 10–3, 4,9 × 10–4, 1,48 × 10–3, до 9,5 × 10–4.
Предпоследнее значение
соответствует моменту времени, когда уже существовала не только Юпитерианская
Земля, но и Солнечная Луна, и согласно уравнению [3]
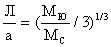 , (26) , (26)
где Л — расстояния точек
Лагранжа от Юпитера,
положение
двух указанных точек Лагранжа находилось за пределами области, отстоящей от
Юпитера на ± 18 × 105 км или 26 радиусов Юпитера, при расстоянии «а» между
компонентами двойной более (2,13 ¸ 2,3) × 107 км, то есть более 0,14 астрономической единицы. Но «а»
вряд ли было меньше этой величины. Юпитерианские производные всегда
находились и находятся внутри области, ограниченной точками Лагранжа системы
Юпитер—Солнце, т. е. в пределах гравитационного влияния (и влияния
других сил), исходящего только от Юпитера. Солнце не смогло повлиять на форму
траектории юпитерианских производных, и они остались правильными круговыми.
С другой стороны, при всех
перемещениях точек Лагранжа, следовавших за перестройками системы двух звезд,
эти точки всегда оставались в области возникновения и нахождения солнечных
производных. Не случайно эксцентриситеты орбит у его разных планет неодинаковые.
Эксцентриситет орбиты Меркурия составляет 0,206, у Венеры 0,007, у Луны (с
Землей) 0,017, у 2-й производной Солнца, которую заместил Марс, — 0,093.
Обращаясь вокруг Солнца на
разных более близких расстояниях, чем современное, Юпитер искажал траектории
его производных, по сравнению с круговыми, оттягивая Солнце от их
геометрического центра так, что эти траектории обращались вместе с Юпитером
вокруг фокуса (эллипсов) с Солнцем в нем, за счет разницы сил притяжения на
стороне эллипса, где находился Юпитер, и на противоположной стороне.
Такова в общем виде картина
развития вещества и рождения планетных систем двойной звезды Юпитер–—Солнце,
полученная на основе проведенного генетического анализа.
Л и т е р а т у р а
1. Р. Дж. Тейлер.
Происхождение химических элементов. М. Мир. 1975.
2. Соболев В. В. Курс
теоретической астрофизики. М. Наука. 1985. 502 с.
3. Дж. Брант, П. Ходж. Астрофизика
Солнечной системы. М. Мир. 1967. 488 с.
4. Карякин Н. И., Быстров К.
Н., Киреев П. С. Краткий справочник по физике. М. Высшая школа. 1963. 560 с.
5. Зайцев О. В. Недостающий
элемент теории гироскопа. // Фундаментальные проблемы естествознания и
техники. Труды Международного Конгресса — 2000. СПб. СпбГУ, 2000.
6. Перельман Я. И.
Занимательная астрономия. М., Наука. 1966. С. 137.
7. Ходьков А. Е., Виноградова
М. Г. Проблема космических термоударных воздействий на Землю в свете Новой
космогонической теории //Теоретические и прикладные вопросы геологии и
гидрогеологии. Л. ВНИИГ. 1989. С. 143–165.
8. Виноградова М. Г., Ходьков
А. Е. Новая космогоническая теория в решении важнейших проблем
естествознания. Бюллетень МАИСУ № 15, октябрь 2000. С. 65–67.
9. Виноградова М. Г., Ходьков
А. Е. Гравитационные силы как проявление динамики взаимодействия эфира с
веществом // Развитие классических методов исследования в естествознании.
Проблемы исследования Вселенной. Вып. 17. СПб. РАН. 1994. С. 78–85.
M. G. Vinogradova
THE GENETIC ANALYSIS of FEATURES
DEVELOPMENTS of PLANETARY SYSTEMS
Of CLOSE DOUBLE STAR the Jupiter-Sun
It is necessary to clarify, what way of a star lose a mass by and will
reject in an interstar-shaped medium substance, synthesized in them, [1].
Planetary nebulas - more serious applicants for being a place, where
the “useful output (exit) “ of elements happens ... Planetary nebulas - are
objects consisting of a star, enclosed gas envelope, which was doubtlessly thrown
out earlier from a star [1].
The study of modifications of a spectrum of a dense envelope New of
Gerkules has shown, that the mentioned envelope can be presented as
"disk", gyrating around of a hot star with a velocity of the order
of 500 km | s , with
availability in an envelope of clots of a substance... [2].
Рaragraph I
About methods* of the genetic analysis of mechanical parameters of
rotation of derivatives of star-shaped evolution
The given analysis does not claim for an absolute exactitude of
obtained figures, but it the purpose - to show genetic communication
(connection) of mechanical parameters of the heavenly sky bodies derived from
envelopes, thrown out by two close stars, and a past stage planetary nebulas,
and to restore on it (her) a main outline of process of evolution of a Solar
system [7].
The separation of envelopes from a star happens owing to change of
modes of аtomformation under an operation of a leaps neutrinos of pressure in
a zone of star-shaped transformation, under an outside envelope of a star,
where there are radial forces, directed from its centre acting on elements of
a mass an envelope [8]. Carrying out an envelope out NEUTRINOS streams there
are more intensive flowing to a star of radio streams creating forces of gravitation.
The force of a separation an envelope from a "new" star on
Sobolev V. V. [2] should be not less force of an attraction on a Newton an
envelope a mass m to the rest of a star-shaped mass M:
F sep > g.
m . M / r2 ,
where r - radius of a star after loss an envelope,
g - Gravitational constant 6,
67. 10 -8 cm 3 /
g. s2.
From expression for impulse of a force of a separation an envelope it
is possible to define (determine) a lower rate of a velocity V r
of an ejection of substance of a star during a dumping an envelope
F sep . t = m . V r ,
whence V r > g
. ρ . 4/3 π . r . t ,
where ρ - denseness of
substation of a star,
t - duration of development of a strain of explosion.
Further we shall remark, that polar areas an envelope of a star after
a separation move is parallel to an axis it of rotation, not saving a rotary
moment of a star, as their moments of inertia NEGLECTFUL are small. Movement
(traffic) of polar parts an envelope here to consider we shall not be.
The equatorial part an envelope surrounding a star as a ring, owes for
want of ejection of an identical force of explosion on a perimeter save
ring-shaped, more correct, toroidal form. For want of it due to a central
character of the acting forces of a separation of a trajectory of fragments
of an equatorial part the envelopes should be flat curve lines located in an
equatorial plane of a star, as taking place through centre of an operation of
forces. The rotating star for want of dumping an envelope informs it (her)
the certain impulse of rotation (moment of an amount of movement (traffic)),
which for want of absence direct effects remains in the characteristic
causing quite certain parameters of rotary movement (traffic) of the formed
satellite as of derivative its evolution: a size of an orbit and angular
velocity ω.
Impulse of rotation L of heavenly sky fields, as the part of impulse
of rotation of a parent star, can be changed only for want of direct contact
to other sky field, for example, in collision, in which the redistribution of
impulse of rotation is carried out.
Inertness of gyrating of a sky body is evaluated it by a moment of
inertia I, dependent apart from of a mass of a sky body still from square of
its radius of inertia.
So, the element m of a mass of a star in its equatorial part under an
operation of a force of a separation is thrown on some distance from an axis
of rotation of a star r > r
star and simultaneously turns
in a plane of an ejection on some angle
φ (fig. I).
Fig. 1. Movement of the thrown
out single element of a mass
in polar coordinates (r; φ) in an
equatorial plane of star:
V r , V φ = ω x ґ , F φ = 2 ω x V r, F r = - ω 2 r
For want of study of movement (traffic) the dropped star an envelope
recommends simultaneously to take into account and possible (probable)
further acceleration an envelope throwing from a star by substance and
braking by its interstar-shaped medium, decrease (reduction) of its velocity
and in some cases a strain [2]. If the envelope will be rejected inside
planetary nebula, then it braking
especially is essential [2].
Main brake the envelope receives from the arisen force of inertia -
response on initial acceleration.
After exhaustion internal neutrinos pressure of a zone of star-shaped
transformation the element of a dropped envelope begins to move on inertia,
testing braking from flowing to a star of
ether streams, simultaneously is gravitational holding it about a
star. Per unit of a mass the envelopes with purchase by her (it) of a radial
velocity V r act the following forces of inertia: in a radial
direction - 1 - centrifugal F c ,
2 - KORIOLIS force connected to the circuit velocity Vφ and directed
against centrifugal; in an environing direction - 3 - KORIOLIS force F φ, connected with a radial velocity V r,
decreasing together with it (her) up to zero and directed in the side of a
circuit velocity. There is radial
brake of a gravitational nature because of overweight throwing to radio ether
streams above shielded by a star [9]:
F br = 2/3 g. ρ star . d star ,
where ρ star and
d star - denseness of substance and diameter of a star.
Radial and
circuit denseness of forces of inertia - braking F r and
rotary F φ:
F r = F c + F r kor = ω 2.
r -
2 ω x V φ = - ω 2 r , (1)
F φ = 2 ω x V r . (2)
Due to slowing down, V r - ω
2 (r orb – r star)
. t = 0 (2a)
The radial movement (traffic) of elements an envelope on a radial
coordinate r orb (radius of an orbit), where V r = 0,
ceases. The equation (2а) shows, that r orb depends on an initial
velocity of an ejection, size of a star and angular velocity it of rotation
before an ejection.
For the star the loss by her (it) an envelope passes not without
leaving a trace: at it (her) the own moment of inertia decreases as both at
the expense of loss of a mass, and at the expense of a diminution of a radius
of gyration.
On each stage of development of a star finished by a dumping of the
next envelope, material system - the star with one parameters (radius of
sphere, denseness of substation, mass, angular velocity of rotation) will be
transformed to a new material system: a star with other parameters and
dropped envelope. The elements last, being transformed in a planetary sky
field or ring separated asteroids, remain genetically connected with
parameters of a parent star in a moment (up to) a dumping of the given
envelope. This genetic communication (connection) is not exposed to
modifications because of a dumping by a star of consequent envelopes.
Really, according to a conservation law of momentum of quantity of
movement [4] derivatives with time from impulse L of rotation of a material system of
rather any motionless point is equal to a general (common) moment M of all
forces (of the rather same point) acting on a material system:
d L | d t = M, or. d (r x m V) | d t = r x F . (3)
The initial material system - star, which should drop an envelope, is
exposed to effect of central forces it of a separation, which have not a
moment of a rather motionless point - centre of a mass of a star. At the same
time with an actuality ejection of an outside stratum on all spherical
surface and uniform a diminution of a radius of sphere the centre of a mass
of a star should remain on the place,
that excludes origin of additional rotary moment of forces.
Then for a considered star d L
/ d t = 0 and L = const. The constancy of impulse of rotation requires
(demands), that L stars up to a dumping an envelope without losses should be
transformed to impulse of rotation of a new system.
Let's show, that the angular velocity of rotation ω of an element of a mass of a dropped envelope is it genetic
characteristic lasting angular velocity of rotation of a star up to an
ejection.
For this purpose we shall analyze the forces, acting on a single
element of mass of a dropped envelope, -
forces of inertia F r and
F φ under the equations (1) and
(2). All forces of inertia F r are central forces, because they
pass through a motionless point - centre of a mass of a star. At the expense
of them the modification of impulse of rotation of a driven element of a mass
of a dropped envelope can not happen. Impulse of rotation L of a driven mass
m changes at the expense of an operation KORIOLIS force of inertia F φ, possessing a moment
M = r x F φ = r x 2ω x V r
x m regarding a rather motionless point.
After definition (determination) of the left part of the equation (3) for a
driven mass m:
d (I . ω)
| d t = d (m . r 2 . ω)
| d t .
And as a result it of transformation the equation is obtained
r 2 . d ω | d t + ω . 2 r . d r | d t = 2 ω .V r . r .
It the solution by transformation gives final expression
r 2. d ω | d t + ω . 2 r . d r | d t = 2ω .V r . r .
From which follows, that r2
.d ω | d t = 0
and
ω = const
at r ≠ 0 is a constant magnitude on a path of
following of an element of a mass of a dropped envelope remaining in sizes
received from a star at the moment of the given ejection.
Let's define impulse of rotation of a star up to a dumping an
envelope:
L star = I star . ω , (4)
where
I star = M star .
r star2 | 4 = 1/ 3 . π .ρ . r star5 .
Let's define impulse of rotation of a new system:
L sys = I’ star
. ω’ + ( I m
+ a 2 . M’ star . m /
M’ star + m) . ω , (5)
where Mstar - mass of star, I’ star and I m
- moments of inertia of rather parallel axes which are taking
place through centers of masses of a "new" star and the element m a
masses of a dropped envelope, which not only rotates around of an external
axis, but also turns about the own axis with a radius of gyration г/2 (both
up to an ejection, and after him (it)):
I’ star = 1/3 π .ρ’ r’ star
5 , I m = m . r 2 / 4.
The second in brackets - moment
of inertia of a common sky field of a rather new parallel axis which is
taking place through their common centre of masses, where a – distance between polar axes of centers of two
mass M’ star and m [4].
The parameters of both stars the Jupiter - Sun on each stage of
development after a dumping of each envelope are defined (determined) from
the equation
L star = L sys. (6)
For want of it appears to an evaluation about magnitudes of the
members of the equation (5), then the second term has the negligible order of
a smallness, and the account (record-keeping) of its third addend for want of
solution of the equation (6) ensures greater exactness on ( 1 – 5 ) %. The practical calculations on
a solution of the equation (6) are executed as with allowance for of third
term (5), and without him (it) (for a
comparison).
The account on the indicated technique for want of ρ Jupiter = 1,33 and ρ ¤ = 1,4 g/cm3 does not
take into account a modification of a denseness of substance of a star during
evolution, as there are no rather authentic information about this
modification, though from indirect reasons follows, that r star
during evolution should grow: the denseness of substance it of derivatives,
and consequently dropped envelopes sequentially grows: at Jupiter from 1,7 up
to 5,52 g/cm3, at the Sun from 2,20 up to 5,30. The magnitude of a gravitational constant
as is accepted not changed in time, though it and is not indisputable.
Рaragraph 2
Jupiter with him derivatives
The account is conducted back in time, from 7-th to the 1-st
derivative.
7 - th derivative - Amaltey.
Angular velocity of the circulation
ω 7 = 2π
radian
/ (11 h 57 minutes) there is an angular velocity of rotation of Jupiter up to
a dumping the 7-th envelope. The angular velocity of rotation of Jupiter
after a dumping the 7-th envelope makes 2π radian/ (9 h 50
minutes) . With allowance for а 7 = 2,5R Jupiter the
equation (6) for the 7-th stage of development of Jupiter is decided
(solved).
It the solution as with allowance for of last addend, and without him
(it), gives a size of Jupiter before a dumping the 7-th envelope
R J6 = 1,04 R J7 = 0,74 . 1010 cm.
Mass of Jove up to a dumping the 7-th envelope or after a dumping the
6-th envelope
MJ6 = 1,125 MJ,
where МJ - modern mass of Jupiter.
6-th derivative - Earth.
The angular velocity ω’ 6 has undergone it
of own rotation a modification on a comparison with genetic because of
collision of the Earth with the Moon and purchase of declination on = 23,5◦ to an initial axis of rotation parallel axis
of rotation of Jupiter [7]. The radius of the circulation of the Earth around
of Jupiter is found as for Kepler orbit for want of genetic angular velocity
of the circulation ω 6 = ω’6 / cos2 = 2π / 19 radian/h
as a 6 = 2,5 . 10 10
cm = 3,5 R J.
The equation (6) for the 6-th stage of development of Jupiter after
its solution gives a size of Jupiter before a dumping the 6-th envelope
R J5 = 1,145R J = 0,815. 10 10 cm,
and disregarding of last addend R J5 = 1,141 R J.
Mass of Jupiter up to a dumping 6-th or after a dumping the 5-th
envelope:
M J5 = 1,5 MJ.
On simplified variant M J5 = 1,485 M J.
5 - th derivative - Mars.
Angular velocity of rotation of Mars ω = 2 π / 24,6 radian / h could divergence
from genetic at the moment of a modification of an angle of declination of
equator up to 25◦ to a plane it of an orbit [6] (because of
collision from the 2-nd derivative of the sun [7]).
As the Earth and Mars should arise in an equatorial plane of Jupiter,
which equator is inclined to a plane it of an orbit on 3◦,
the modification of an angle of declination of Mars of an axis of rotation
from initial (originally) was carried out in limits a = 25 - 3 = 22 ◦ or 0,38 radians. For
Kepler orbit with genetic ω 5 =2 π / 33,5 r / h
is the radius of the circulation a = 3,6 . 10 10 cm= 5 R
J . The equation (6) for the
5-th stage of development of Jupiter gives
R J4 = 1,282R J = 0,912. 10 10 cm.
Mass of Jove up to a dumping 5-th or after a dumping the 4-th envelope
on an approximate evaluation
M J4 = 1,4M J5 = 2 M J,
On a more point evaluation M J4 = 2,1 M J.
4 - th derivative - Io.
The parameters of the circulation Io make a = 4,22 .10 10 cm and
ω = 2π /42,5 radian / h.
The equation (6) for the 4-th stage of development of Jupiter after
its point solution gives a size of Jupiter before a dumping the 4-th envelope
R J3 = 1,345R J = 0,957. 10 10 cm, approximately R J3 = 0,939. 10 10 cm.
The mass of Jupiter up to a dumping 4-th or after a dumping the 3-rd
envelope on an approximate evaluation M J3 = 1,15M J4 =
2,3 M J, is
more exact M J3 = 2,43 M J.
3 – d derivative - Europe.
The parameters of the circulation of Europe make a = 6,7. 10 10 cm and ω
= 2 π
/
85,2 radian / h.
From the equation (6) for the 3-rd stage of development of Jupiter
follows, that R J2 = 1,545. R J = 1,1. 10 10cm,
the approximate evaluation gives R J2 = 1,08. 10 10 cm.
The mass of Jupiter up to a dumping 3-rd or after a dumping the 2-nd
envelope accordingly M J2 = 3,68M J and is less exact M
J2 = 3,5 M J.
2 - nd derivative - Hanimed.
The parameters of the circulation Hanimed make a = 10,71. 10 10 cm and ω = 2π / 171,7
radian / h.
From the equation (6) for the 2-nd stage of development of Jupiter
follows, that R J1 = 1,78. R J = 1,26. 10 10 cm, the approximate evaluation gives R J!
= 1,24 . 10 10 cm.
The mass of Jupiter up to a dumping 2-nd or after a dumping the 1-st
envelope accordingly M J1 = 5,64M J and is less exact M
J1 = 5,32 M J.
1-t derivative – Kallisto
The parameters of the circulation Kallisto make a = 18,8. 10 10 cm and ω = 2π / 400,5 radian / h..
From the equation (6) for the 1-st stage of development of Jupiter
follows, that R J0= 2,11. R J = 1,5.10 10 cm, the approximate evaluation gives R J0
= 2,10 R J = 1,47. 10 10 cm.
The mass of Jupiter up to a
dumping the 1-st envelope made on a more point evaluation M J0 =
9,39M J and less precisely M J0 = 9,26 M J.
Paragraph 3
The Sun with his derivatives
The account should be conducted back in time, from 7-th to the 1-st
derivative. However among 7 the solar derivatives on 4 dropped envelopes are
not present rather authentic information about their mechanical parameters of
rotary movement (traffic). Including on yet not exhibiting itself by the 7-th
derivative - Volcano on Leverye,
rendering perturbations from orbital movement of Mercuriy, 4-th
dropped envelope - ring metal asteroids, 2-nd dropped envelope - ring of coal asteroids and 2-nd planet of the
Sun and, at last, 1-st envelope – by hydrogen – helium derivative with unknown destiny. In this
connection reliability of the executed accounts should be checked by
definition(determination) of points of the Lagrange of two stars of Jupiter-
Sun during evolution of a double system, which site limits a scope of an
attraction of each of two stars, and the instability of balance of forces is
the reason of collision of the competitors on intersected orbits of
derivatives of two stars, especial for want of reorganizations of a system.
In a solution of the equation (6) for development of the Sun the role
of the last member (5) becomes neglectful is small, as the masses it of
derivatives neglectful are small in a comparison with M ☺.
7-th divative - from synthesis
of the 5-th period of elements
As parameters an envelope dropped by the Sun in the time, least remote
from us (227 million Years ago), are even unknown, by analogy of decrease of
sizes of orbits from 3-rd to 4-th to solar periods the rough radius of an
orbit of a considered envelope can be accepted 0,285 а.u. = 61,2 R ☺. An angular velocity of the circulation an envelope
is defined from the law Кеpler for want of а 7 = 0,285 а.u. as ω 7 = 2π /
58 radian/day. This significance is rough
velocity of the circulation of the 7-th envelope, dropped by the sun, for
want of which dumping Sun has lost mass and has increased angular velocity of
rotation up to.
The equation (6) for the 7-th stage of development of the Sun after
its solution, both point, and approximate gives a size of the Sun up to a
dumping the 7-th envelope:
R ☺6 = 1,18 R ☺ = 8,26. 10 10 cm.
Mass of the Sun up to a dumping 7-th or after a dumping the 6-th
envelope:
M ☺6 = 1,64 M ☺.
6 - th derivative - Mercuriy
Angular velocity of the circulation of Mercury ω = 2π / 88 radian/day
and large semiaxis of an orbit а 6 = 0,38 аuе. = 81,7 R ☺.
The equation (6) for the 6-th stage of development of the Sun after
its solution gives for a size of the Sun up to a dumping the 6-th envelope:
R ☺5 = 1,28 R ☺ = 8,96. 10 10 cm.
Mass of the Sun up to a dumping 6-th or after a dumping the 5-th
envelope:
M ☺5 = 2,097 M ☺.
5 – th derivative Venus
- from synthesis of the 4-th
period
Angular velocity of the circulation of Venus ω = 2π/224 radian/day , large
semiaxis of an orbit а 5 = 0,72 а.u. = 154,8 R ☺.
The equation (6) for the 5-th stage of development of the Sun after
its solution gives a size of the Sun up to a dumping the 5-th envelope:
R ☺5 = 1.55 R ☺ = 10,85. 10 10 cm.
Mass of the Sun up to a dumping 5-th or after a dumping the 4-th
envelope M ☺4 = 3,72 M ☺.
4 -th dropped envelope
(М-asteroids ring)
It is inconveniently to receive point significances of genetic
parameters of the circulation of metal asteroids. The cycle of revolution of
metal asteroids makes on the average magnitude ω4 about 300 days,
that there corresponds (meets) an
orbit by Kepler with an average radius of the circulation 0,87 а.u.
Increase of rotation of the Sun in an outcome of a dumping the 4-th
envelope could make 300/224 = 1,339 times. From the equation for impulse of
rotation of the Sun it is possible to receive, that it the size before the
4-th flare made R ☺3 = 1,06 R☺4.= 11,5. 10 10 cm.
The mass of the Sun up to a dumping by fourth or after a dumping the
3-rd envelope made
M ☺3 = 1,19 M ☺4 = 4,42 M ☺.
3 – d dropped envelope (ring
of S-asteroids and Moon) from
synthesis o
the 3-rd period
The angular velocity of own rotation of silicic asteroids is difficult
to define because of a smallness of their sizes, and from a comparison ω 3 = 2π / 27,3 radian/day of the Moon
with ω 4 = 2π /300 radian/day follows(~is necessary) to make a
conclusion that after a dumping the 3-rd envelope the moment of inertia of
the Sun sharply has increased in 300/27,3 = 11 times. This phenomenon can
mean an absorption by the Sun of strange mass which has increased in the
total a mass of a star presumably in 1,62 3 = 4,25 times.
Size of the Sun before the 3-rd flare
R ☺2 = R ☺3 /1,62 = 7,09. 10 10 cm.
i.e. almost as modern, and mass
M ☺2 = 4,42 / 4,25 = 1,039 M ☺.
The impulse of rotation or amount of rotation of the Moon in the 3-rd
envelope at once after an ejection is evaluated by the equation (5) of two
members:
L M = L own M + L M-S ,
From which the first member has the negligible order of a smallness.
The amount of rotation of a double planet Earth - Moon is evaluated by
the equation (5) of 5-th members:
L E-M = L own E
+ L own M + L sys E-M + L S-E
+ L S-M
,
from which defining there are two last in a comparison with a
negligible smallness remaining.
2 – d dropped envelope – a ring
of coal asteroids with
splinters
of carbonaceous planet - from
synthesis of the 2-nd period
From the second envelope, dropped by the Sun, was derivate a powerful
ring of coal asteroids and
carbonaceous planet destroyed in collision with Mars.
It shows comparison of their impulses of rotation.
Moment of inertia and impulse of rotation of the 2-nd planet of the
Sun with a unknown mass m 2 are expressed with alignment to a mass
of the Moon through a mass of Mars substituting 2-d planet on its orbit (r mars =
3,35. 10 8 cm, r 2 = 1,7. 10.7 cm, ρ mars = 3,95 g/cm 3 , ρ 2 = 2,2 g/cm 3):
M 2 = M mars / 13,7.
Hypothetical impulse of rotation of the 2-nd planet obtained by her
from the Sun:
L’ 2 = 2π. m 2. r 2 2 /4. 100
day +
2π. m 2 .a 22 /100 day ,
where
first addend is possible to
lower for it smallness, as well as in impulse of rotation of Mars on orbit of Jupiter TURNING around protosun.
Increase of rotation of the Sun during a dumping the 2-nd envelope:
100 сут/27 сут = 3,7 times.
Before a dumping the 2-nd envelope the Sun had a size:
R ☺1 = 3,7 1/5 . R ☺2 = 1,3. R ☺2 = 9,2.
10 10 cm.
Mass of the Sun before a dumping second and after an ejection of the
first envelope:
M ☺1 =2,19. M ☺2 = 2,27. M ☺.
I-t dropped envelope - from synthesis of the 1-st period
Rather I-t derivative of the Sun –hydrogen-helium planet, the comets
or separated ASTEROIDS are not known neither mass, nor character of the
circulation.
If to accept a hypothetical angular velocity of rotation of the Sun up
to a dumping I-t envelope ω 1 = 2π /300 radian/day , so increase it
angular velocity of rotation in time I-t of flare made 300/100 = 3 times.
From the equation for impulse of rotation of the Sun it is possible to
receive it a hypothetical size up to an ejection I-t an envelope:
R ☺0 = 3 1/5
R ☺1 = 1,642. R ☺ = 11,5. 10 10 cm .
And the initial mass could make
M ☺0 = 1,95. M ☺1 = 4,43. M ☺.
About possible transitions of points of the Lagrange in process
developments of a double star the JUPITER-SUN
For a system two addressed one rather other of heavenly skew fields
there are 5 points of the Lagrange [3], two of which lay on direct,
connecting sky fields.
Transition of points of the Lagrange in a close system the JUPITER-SUN
should inevitably happen in connection with a modification of ratio of masses
of stars. The ratio of masses of components M J /M ☺ varied spasmodically in the following
significances: from 2,1.10 -3, 4,9.10 -4, 1,48. 10 -3,
up to 9,5. 10 -4.
The penultimate significance corresponds (meets) to an instant, when
already there was not only Jupiterian Earth, but also Solar Moon. And
according to the equation [3]
lag/a =( M J
/ 3 M ☺)1/3 ,
where lag - distance of points
of the Lagrange from Jupiter,
the position of two indicated points of the Lagrange was outside area,
distant from Jupiter on 18. 10 5 km or 26 radiuses of Jupiter, for want of
distance "а" between components double more (2,13 - 2,3). 10 7 km, that is more 0,14 astronomical units. But
" a " hardly was less this magnitude. Jupiterian derivatives always were and are
inside area limited to points of the Lagrange of a system the
Jupiter-Sun, within the limits of
gravitational influence (and influence of other forces), outgoing only from
Jupiter. The Sun could not affect the form of a trajectory Jupiterian
derivatives, and they have remained correct circular.
On the other hand, for want of all transitions of points of the
Lagrange following reorganizations of a system of two stars, these points
always remained in the field of origin and determination of solar derivatives.
Not accidentally eccentricities of orbits at it of different planets unequal.
The eccentricity of an orbit at Mercuriy makes 0,206, at Venus 0,007, at the
Moon (with the Earth) 0,017, at the 2-nd derivative of the Sun, which was
substituted with Mars, - 0,093.
Addressing around of the Sun on different closer distances, than
modern, Jupiter distorted trajectories it of derivatives, on a comparison
with circular, delaying the Sun from their geometric centre so, that these
trajectories were converted together with Jupiter around of a focal point
(ellipses) with the Sun in it (him), at the expense of a difference of forces
of an attraction on the party of an ellipse, where there was a Jupiter, and
on the opposite party.
Literature
1. R. J. Teyler. An origin of
chemical elements. Мoscow. World.
1975.
2. Sobolev V.V. Course of a theoretical astrophysics. Мoscow. Science.
1985. 502 p.
3. J. C. Brandt , P. W. Hodge. Solar system astrophysics. Мoscow.
World. 1967. 488 p.
4..Khod’kov A.E., Vinogradova M.G. The Problem of cosmic termo-shock
effects on the Earth in light of New
cosmogonic theory // Theoretical and applied problems of geology and
hydrogeology. L. All U I for S R of G. 1989. P. 143-165.
5. Vinogradova M.G., Khod’kov A.E. The New cosmogonic theory in a
solution of major problems of natural sciences. The report International
Academy “МАИСУ”, № 15, October 2000.
P. 65-67.
6.Vinogradova M.G., Khod’kov A.E. Gravitational forces as
manifestation of dynamics of interaction of an ether with substance //
Development of classical methods of a research in natural sciences. Problems
of research of the Universe. Issue.
17. S-Pb. “НИИРЭК”. 1994. P.
78-85.
|

