Фенотипической адаптацией называется свойство живых организмов приспосабливаться к изменяющимся условиям внешней среды [ 1 ].

Реакции фенотипической адаптации условно могут быть разделены на два  вида:

1. Оперативную фенотипическую адаптацию, в результате которой организм путем соответствующих физиологических реакций быстро и непрерывно реагирует на  все кратковременные факторы, влияющие на его жизнедеятельность. При этом средние значения показателей его функциональных систем не изменяются.

2. Устойчивую фенотипическу адаптацию, в результате которой в условиях длительного воздействия на организм факторов внешней среды произошли такие перестройки его функциональных систем, при которых их средние показатели изменились.

Проблемам фенотипической адаптации посвящено большое количество научных работ. Однако в основном они содержат результаты всевозможных наблюдений либо различные теории, предлагающие те или иные научные объяснения наблюдаемым биологическим явлениям [ 1, 3, 5, 6, 8, 9], поэтому природа адаптации и ее основные закономерности до сих пор неясны.

Настоящая работа посвящена определению природы адаптации и ее основных законов путем анализа биологических процессов, исходя из принципов жизнедеятельности живых организмов как открытых термодинамических систем.

Все процессы в живых организмах происходят не непрерывно, а в виде периодических циклов, содержащих  чередующиеся фазы процессов синтеза и расщепления, причем в основном эти процессы являются ферментативными управляемыми реакциями с положительными и отрицательными обратными связями [ 2 ]. Именно этим путем организмы обеспечивают свое устойчивое термодинамическое неравновесное состояние, проходя в течение каждой фазы три термодинамических состояния: равновесное, слабо неравновесное и сильно неравновесное [ 4, 7 ].

Поскольку клетка является «единицей жизни» и одновременно полноценным организмом, проведем анализ ее поведения при воздействии на нее нагрузки, вызывающей увеличение объема биохимических реактивов (в основном АТФ) и скорость реакций.

При воздействии такой нагрузки на клетку для сохранения жизнеспособности - устойчивости ее неравновесного термодинамического состояния, в ней будут активизированы ферменты, повышающие в течение фазы расщепления скорость биохимических ферментативных реакций и количество участвующих в ней реактивов. При уменьшении количества реактивов до критического значения реакции расщепления остановятся, и начнется вторая фаза, в течение которой в клетке начнут синтезироваться в увеличенном количестве реактивы и ферменты, участвующие в биохимических реакциях первой фазы цикла. Далее эти процессы будут многократно повторяться за все время действия нагрузки.

При снятии нагрузки активность ферментов начнет уменьшаться. В результате этого скорость биохимических реакций и объем реактивов также начнут уменьшатся до исходного уровня.

Реакции на нагрузки многоклеточных организмов, включая организм человека, являются интегральным результатом функций отдельных клеток. Поэтому далее будем рассматривать закономерность биохимических реакций на уровне целостного организма человека.

Для определения общей закономерности прохождения биохимических реакций рассмотрим закономерность реакции организма человека на одиночную нагрузку в виде прямоугольного импульса.

Здесь необходимо указать, что теоретически закономерность ферментативных реакций должна подчиняться закону Михаэлиса – Ментен. Однако этот закон описывает только одну каталитическую реакцию, и то на нескольких не совсем реальных допущениях, в частности таких, как отсутствие в растворе других форм фермента.

В нашем же случае необходимо анализировать закономерность изменений  функционального сдвига как конечного совокупного результата всего комплекса биохимических реакций, участвующих  в его формировании. 

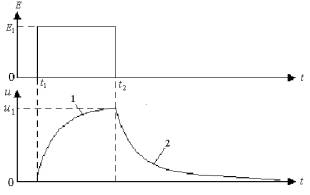
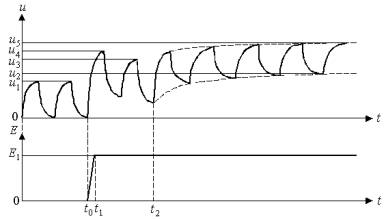
На рис.1 представлен упрощенный график некоторого общего случая закономерности изменений функционального сдвига u при воздействии нагрузки E₁ прямоугольной  формы.

Рис.1. Упрощенный график закономерности изменений функционального сдвига u

при воздействии нагрузки прямоугольной формы E₁.

Как  видно  из  рис.1,  при  воздействии  на организм нагрузки E₁ в промежутке времени от t₁ до t₂, в нем возникает и начинает нарастать некоторый функциональный сдвиг u, который достигает своего максимального значения u₁ в момент прекращения действия нагрузки t₂  (кривая 1). После прекращения действия нагрузки E₁ функциональный сдвиг u начинает восстанавливаться, приближаясь к оси абсцисс по закону, близкому к  экспоненциальному. Отсюда следует, что определить точное время восстановления функционального сдвига t, при котором u = 0, невозможно.

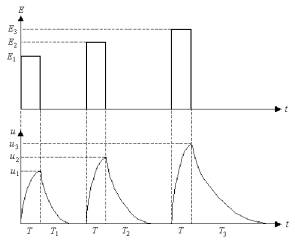
Рассмотрим зависимость величины изменений функциональных сдвигов u от изменения величины и длительности нагрузки E.

На рис.2 показаны закономерности изменений функциональных сдвигов u при разной величине нагрузки E, но одинаковой длительности.

Рис. 2.  Зависимость изменений функциональных сдвигов u

от изменения величины нагрузки E.

Как видно из рис.2, с увеличением абсолютной величины нагрузки E, действующей в течение равных промежутков времени T, величина функциональных сдвигов u возрастает. При этом возрастает и время их восстановления  T₁, T₂ и T₃.

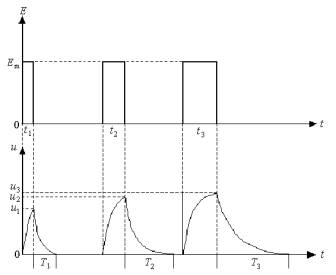
Рассмотрим зависимость изменений величины функциональных сдвигов u от длительности действия нагрузки E_m.

На рис.3 показаны закономерности изменений функциональных сдвигов u при разной длительности действия, но равных по величине нагрузок E.

Рис. 3.  Зависимость изменений величины функциональных сдвигов u

от длительности действия  нагрузки E_m.

Как видно из рис.3, с увеличением длительности воздействия t одинаковой по величине нагрузки E_m величина функциональных сдвигов u возрастает. При этом возрастает и время их восстановления  T₁, T₂ и T₃.

  Отсюда следует, что время восстановления T функциональных сдвигов E зависит как от величины нагрузки u, так и от длительности ее воздействия t.

При незначительных нагрузках, которые назовем нормальными,  организм путем изменений скорости и объема биохимических реакций, внешне проявляющихся в виде функциональных сдвигов, достаточно быстро обеспечивает устойчивость неравновесного термодинамического состояния организма.  При снятии таких нагрузок восстановление функциональных сдвигов также происходит достаточно быстро.

При очень большой и/или очень длительной нагрузке для сохранения устойчивого неравновесного термодинамического состояния циклы биохимических реакций в клетках начинают работать в режимах, близким к предельным, при которых за счет ферментов достигаются максимальные скорости биохимических реакций и объем участвующих в них реактивов. Это выражается в значительных функциональных сдвигах. После снятия таких нагрузок организму требуется достаточно большое время для их восстановления.

При воздействиях  на организм нагрузок, превышающих предельно допустимые, достаточно велика вероятность повреждений, заболеваний или гибели организма.

Таким образом, нагрузки можно разделить на три категории: нормальные, повышенные и непереносимые со следующими определениями:

-      нормальные нагрузки – нагрузки, наиболее комфортные для организма;

-      повышенные нагрузки – нагрузки, которые могут  воздействовать  на  организм  без последствий лишь ограниченное время;

-      непереносимые нагрузки – нагрузки, которые могут привести организм к заболеваниям, травмам, либо к гибели.

Изменения в ходе биохимических реакций приводят и к различным физическим изменениям как в клетках, так и в органах,  системах и в организме в целом.

Изменениям подвергаются такие параметры организма, как масса, объем, формы, геометрические размеры, выносливость, физическая сила, память и др.

Следует отметить, что плазматическая мембрана, органелы и другие элементы клеток по своим физическим характеристикам достаточно пластичны. Поэтому в процессе  жизнедеятельности при воздействии нагрузок их размеры и формы постоянно меняются в определенных пределах, не приводящим к каким-либо нарушениям или повреждениям их структуры. Повреждения  могут наступить лишь в результате действия достаточно больших либо быстро изменившихся нагрузок.

Как уже было указано, если нагрузка по своей величине соответствует нормальной или повышенной, возникает редко и на короткое время, то каждый раз после ее окончания режим работы клетки восстанавливается до исходного уровня.

Если же такая нагрузка начинает действовать часто и/или длительное время, то в результате многочисленных циклов метаболизма при каждом из них в клетке происходит накопление незначительных физических изменений. В результате этого в клетку начинает уже постоянно поступать повышенное количество продуктов питания, а в биохимических реакциях постоянно участвовать повышенное количество реактивов. В результате в клетке произойдут определенные физиологические перестройки, после чего такой режим функционирования клетки станет для нее нормальным, и он будет сохраняться все время, пока на клетку действуют указанные нагрузки. График такого процесса изображен на рис. 4.

Рис.4.  Процесс устойчивой фенотипической адаптации

u – средняя величина функционального сдвига,  t – время, u₁ – средняя величина  

функционального сдвига до воздействия нагрузки, u₂ -  средняя величина 

функционального сдвига после фенотипической адаптации,  t₁ – время начала  

воздействия    нагрузки, t₂ – время завершение процесса адаптации, E – нагрузка,

E₁ – средняя величина нагрузки.

Как видно из рис.4, в результате фенотипической адаптации за время t = t₂ – t₁ действия нагрузки E₁ произошли изменения в ходе биохимических реакций, вызвавшие в организме  определенные перестройки, после которых среднее значение колебаний функциональных сдвигов u₁ увеличилось до значения u₂, которое стало постоянным в условиях постоянного воздействия нагрузки E₁.

При длительном снятии нагрузки произойдет фенотипическая адаптация в обратном  направлении.

Необходимо отметить, что в реальных условиях нагрузка не прикладывается мгновенно, а происходит в течение определенного времени. Кроме того, живые организмы реагируют не только на величину нагрузки, но и на скорость ее возрастания.

На рис.5 показан пример графика реальных изменений колебаний функциональных сдвигов u при действии постоянной нагрузки E₁.

Рис.5. Пример графика изменений колебаний функциональных сдвигов u

при действии постоянной нагрузки E₁.

Реакция организма на постоянную нагрузку происходит следующим образом.

Как видно из графика на рис.5, до начала действия нагрузки E₁ размах колебаний функционального сдвига составлял u₁. Нагрузка начинает действовать с момента  t₀, возрастая за время t = t₁ – t₀  от значения  0 до значения E₁.

В первый момент действия нагрузки t₀ размах колебаний функционального сдвига резко вырастает от значения u₁ до u₄. Это объясняется реакцией организма на два одновременно воздействующих параметра нагрузки: величину E₁ и скорость ее  нарастания: v=dE₁/dt.

К моменту времени t₂, поскольку величина нагрузки с момента t₁ не меняется, составляющая колебаний функционального сдвига, вызванная параметром скорости изменения нагрузки, восстанавливается. Далее происходят изменения колебаний функционального сдвига, определяемые только действием величины нагрузки E₁: размах функционального сдвига уменьшается при одновременном увеличении среднего уровня его значения. Причем изменения минимальных,  максимальных и средних значений функциональных сдвигов будет происходить по идентичным законам, соответственно:

u = u_min(1 – e^-kt);  u = u_max(1 – e^-kt);  u = u_ср(1 – e^-kt);

При периодической нагрузке фенотипическая адаптация организма зависит от того, что собой представляет эта нагрузка:  величина, параметры, периодичность и др.

Рассмотрим процессы устойчивой фенотипической адаптации при воздействии различных видов периодических нагрузок.

Воздействие на организм человека нормальной периодической нагрузки прямоугольной формы (реакция организма на скорость изменения нагрузки не рассматривается) .

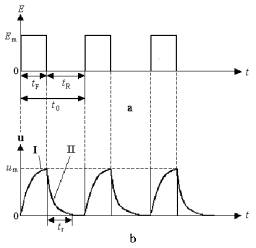
На рис.6 приведены график периодического чередования нагрузок E  (a) и график соответствующих функциональных сдвигов (b).

Рис.6. График колебаний функционального сдвига u от воздействия нормальной периодической нагрузки E_m.

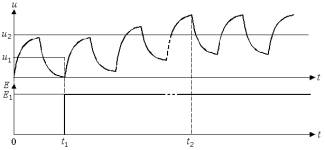
Как видно из рис.6, за время t_F воздействия нормальной периодической нагрузки E_m функциональный сдвиг u за время паузы t_R полностью восстанавливается за время t_r<t_R до исходного уровня. При последующих нагрузках закономерность роста этого функционального сдвига полностью повторяется. 

Рассмотрим случай воздействия на организм периодической повышенной нагрузки E_m, при которой t_r > t_R, представленный на рис.7.  Как видно из графика а на рис.7,  на организм человека периодически, с периодом t₀,   длительностью t_f  и паузой t_R воздействует нагрузка  величиной E_m.

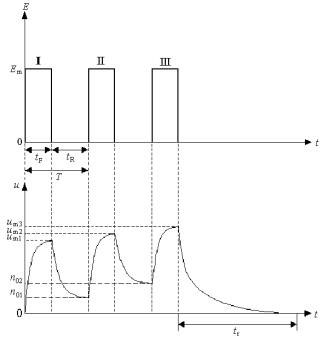
Рис.7. График колебаний функционального сдвига u

от воздействия повышенной  периодической нагрузки E.

Как видно из рис.7, воздействие на организм повышенной нагрузки I величиной E_m и длительностью t_F вызывает функциональный сдвиг u_m1, который не успевает восстановиться за время паузы t_R и к моменту прихода нагрузки II такой же величины  остаточное значение функционального сдвига составляет n₀₁.  В результате действия нагрузки II функциональный сдвиг достигает значения u_m2 > u_m1. который также не успевает полностью восстановиться до прихода нагрузки III и его остаточное значение уже составляет n₀₂. Воздействие нагрузки III вызывает рост функционального сдвига до  значения u_m3. И только в процессе длительного отдыха t_r  функциональный сдвиг u восстанавливается до исходного уровня. Такие случаи роста функциональных сдвигов часто наблюдаются в процессе рабочей недели и их полном восстановлении за выходные дни, при вахтовых графиках работы в экстремальных условиях (неделя через неделю) и др.  В реальных ситуациях изменения размаха функциональных сдвигов как в сторону увеличения, так и  уменьшения зависит от характера нагрузки и соотношения ее параметров с параметрами организма.

Таким образом, благодаря принципу функционирования в виде последовательностей циклов биохимических реакций, живые организмы обладают свойством фенотипической адаптации к изменяющимся условиям внешней среды.

Исходя из изложенного, можно сформулировать сущность свойства живых организмов к фенотипической адаптации:  

Литература

1.                  Анохин П.К. Очерки по физиологии функциональных систем. - М.: Медицина, 1975.- 477 с.

2.                  Биохимия. Под ред. Северина Е.С. М. ГЭОТАП-МЕД. 2003.

3.                  Гаркави Л.Х.,. Квакина Е.Б, Уколова М.А.. Адаптационные реакции и резистентность организма. - Ростов-на-Дону: Ростовский ун-т, 1977. - 109 с.

4.                  Доброборский Б.С. Конец легенды о биоритмах. Личность и культура. 2005.6. С. 24-28.

5.                  Меерсон Ф.З. Адаптация, стресс и профилактика. Наука. М. 1981

6.                  Меерсон Ф.З., Пшенникова М.Г.. Адаптация к стрессовым ситуациям и физическим нагрузкам. - М.: Медицина, 1988. - 256 с.

7.                  Пригожин И., Стенгерс И. Порядок из хаоса: Новый диалог человека с природой .Наука. М. 1986.

8.                  Уголев А.М. Эволюция пищеварения и принципы эволюции функций. Элементы современного эволюционизма. - Л.: Наука, 1985. - 544 с.