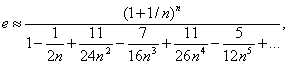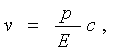<<< Interlibrary

e, a, π, б  сидели на трубе.

          a  упало, б  пропало. Кто остался на трубе?

Наш друг читатель уже догадался, кто там остался.

Известны числа, описывающие мир  в застывшем виде. Не таковы e  и π. Они связаны со всем и в первую очередь  с движением, с явлениями, процессами, объектами. Первое из них – с возрастающими и убывающими. Второе – с периодическими, повторяющимися. Они содержат в себе такой всеобъемлющий космологический смысл, что мы хотим приводить формулы только как иллюстрирующий материал, оставив как их строгий вывод, так и множество других интересных соотношений в качестве возможных упражнений для заинтересованных читателей, которые также захотят что-то опубликовать на эти темы.

Итак, числа e и π – иррациональные, трансцендентные, т.е. не удовлетворяющие каким-либо алгебраическим уравнениям с целыми коэффициентами. Число e = 2.71828… . Оно обладает рядом уникальных свойств, например:

d/dxe^x=e^x,    d/dxe^-x=-e^-x,    d/dx(-e^x)=-e^x,    d/dx(-e^-x)=e^-x,   dⁿ/dxⁿe^x=e^x, …

Эти свойства можно обнаружить всюду, в живой природе, в микромире, в космологии, … . Эффект космологического красного смещения проявляется в частности в том, что при прохождении фотоном  (а также, по-видимому, нейтрино) расстояния r = R = c / H, где R – радиус гравитационного взаимодействия, H – постоянная Хаббла, его длина волны увеличивается, а энергия E, импульс p, частота ν уменьшаются в e раз. Если разделить R на достаточно большое число n равных частей, то эффект для каждой части можно описать соотношением

exp(1/n) ≈ 1 + 1/n,

откуда следует:

Вместо этого для определения e  можно использовать бесконечные ряды:

Эти соотношения приведены во всех справочниках. К сожалению, для определения  e на основе (1) необходимо «астрономическое» значение числа n.

Соттношение, обеспечивающее быструю сходимость к числу e, приобретает после небольших упрощений вид:

Использование каждого дополнительного члена ряда в знаменателе, при фиксированном числе n, которое может быть как положительным, так и отрицательным, позволяет уменьшить неточность примерно в | n| раз.

Однако бесспорным достоинством соотношения (1) является его классический вид и возможность простой интерпретации. От него можно перейти к рассмотрению внегалактического объекта, находящегося на расстоянии r.  Выражения для энергии E регистрируемого фотона в функции первоначальной энергии E₁ ,  для космологического красного смещения  Z   и для расстояния имеют вид:

Еще более интересно перейти от равных отрезков к неравным отрезкам с одинаковыми значениями абсолютного уменьшения энергии микрообъекта. Согласно теории единого поля [ 1 ], движущийся в свободном пространстве микрообъект на каждом отрезке, равном длине волны де Бройля λ = h/p, теряет энергию hH, равную энергии П-фотона (продольного фотона де Бройля). Если это так, то для микрообъектов, находящихся «в свободном полете», получается два набора решений:

§                                       Характеристики частиц, обладающих массой покоя, выражаются через расстояние с использованием гиперболических функций (табл. 1), но при  этом импульс  p в функции времени описывается затухающей экспонентой.

§                                       Характеристики фотонов и нейтрино, т.е. безмассовых частиц, как в функции расстояния, так и времени, описываются экспоненциальными зависимостями.

Таблица 1.

Математическая аналогия между двумя теориями

В то же время это родственные решения, проскольку гиперболические функции выражаются через экспоненты.

Эти же результаты можно получить из уравнения Пуассона [1a]:

представляющего собой закон всемирного тяготения Ньютона с небольшой поправкой в виде ρ_ср. Здесь Ψ – гравитационный потенциал, имеющий размерность квадрата скорости. G – постоянная Ньютона, ρ – распределенная в пространстве плотность вещества, ρ_ср – средняя плотность вещества во Вселенной. Введение поправки в закон Ньютона позволяет разрешить три парадокса классической космологии: фотометрический парадокс Шезо-Ольберса, термодинамической парадокс «тепловой смерти» Клаузиуса-Кельвина и гравтационный парадокс Неймана-Зелигера. При рассмотрении процессов в свободном пространстве это уравнение приводится к виду  

,

т.е.

откуда можно получить уравнение для энергии E микрообъекта, движущегося в таком пространстве по некоторому пути r:

О виде интересующих нас частных решений, которые по крайней мере в случае фотонов согласуются с результатами наблюдений основных классов внегалактических объектов, мы уже говорили. Полученные на этом пути результаты кажутся знакомыми. Аналогичные соотношения были получены в теории расширяющейся Вселенной для случая k=1 (пространство Лобачевского), когда время t, расстояние r (космологический масштабный фактор), скорость расширения v были представлены в функции некоторого  параметра [ 2 ], смотрите здесь в табл.1. На  самом  деле, если пренебречь тем, что масса Вселенной бесконечна, а масса любого микрообъекта мала, следует вспомнить, что энергия – это скаляр, времяподобная величина, импульс – вектор, пространствоподобная величина, характеризуемая в общем случае тремя компонентами, а скорость микрообъекта и скорость «улетания» галактик в теории расширения Вселенной характеризуются соотношениями:

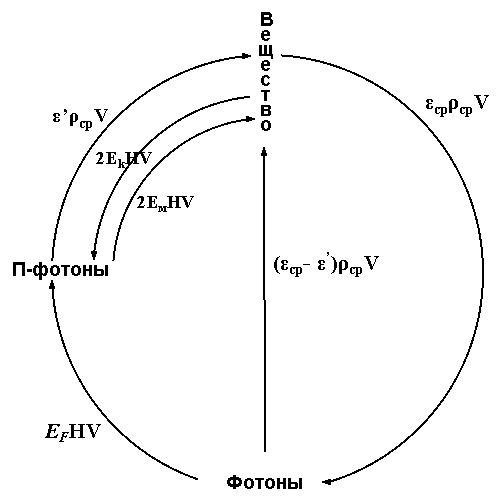
Итак, теория Ньютона с поправкой, таория единого поля и теория расширения Вселенной приводят к числу e, поскольку любая гиперболическая функция выражается через возрастающие и убывающие экспоненты. В случае теории единого поля это объясняется процессами взаимодействия микрообъектов с физическим вакуумом, включающим в себя П-фотоны, концентрация которых, по-видимому, весьма высока [1]. Излучение передает энергию физическому вакууму в виде П-фотонов. Физический вакуум передает энергию веществу в виде П-фотонов. Вещество излучает энергию  в основном в виде фотонов. Помимо этого, движение заряженных частиц в свободном пространстве поддерживает определенный уровень космического магнитного поля (объясняемого эффектами поляризации П-фотонов), которое является передатчиком энергии от одних частиц вещества к другим. Круговая схема преобразоваия энергии представлена на рис.1, где

ε_ср – средняя мощность, излучаемая единицей массы межгалактического вещества в виде микроволновых фотонов, ε^’ – мощность, поглощаемая единицей массы в виде П-фотонов, (ε_ср- ε^’) – средняя мощность, поглощаемая единицей массы внегалактического вещества в виде радиофотонов, E_F – плотность энергии микроволнового фонового излучения,  М Ф И, E_k и E_м – плотности кинетической энергии и энергии космического магнитного поля в межгалактическом пространстве, V – любой достаточно большой объем порядка 10⁸¹ см³. Описание некоторых существенных процессов, охватываемых этой упрощенной схемой, невозможно не только без числа e, но  и без числа π.

Рис.1. Упрощенная схема преобразования энергии во Вселенной.

Литература

1.      Шлёнов А.Г. Микромир, Вселенная, Жизнь. 1-е изд. Под ред. проф. В.И.Почтарёва. СПб. 1995.

1а. Шлёнов А.Г. Микромир, Вселенная, Жизнь. 2-е изд. Под ред. проф. А.К.Колесова. СПб. 1998.

1b. Шлёнов А.Г. и Петров Э.Л. Микромир, Вселенная, Жизнь. 3-е изд. Под ред. проф. А.К.Колесова. СПб. 2003.

1с. Шлёнов А.Г. и Петров Э.Л. www.interlibrary.narod,ru. (Astronomy Department Ns 59, 60, …)

2.   Ландау Л.Д. и Лифшиц Е.М. Теория поля. М. Наука. 1967. с. 440-441.

<<< Interlibrary