С.А. Волков

Доктор технических наук, профессор

Санкт-Петербургский государственный архитектурно-строительный университет

 

РАЗВИТИЕ ТЕОРИИ И КОНСТРУКЦИЙ МЕХАНИЗМОВ ПРАВКИ МЕТАЛЛИЧЕСКИХ СТЕРЖНЕЙ

 

Виды механизмов правки и их особенности

Правильно-отрезные станки могут быть сведены к двум принципиальным схемам (рис.1), тогда как станки, используемые в технологических процессах, могут иметь различное сочетание этих механизмов и их различное количество. Схемы охватывают современные и ранее выпускавшиеся станки отечественных и зарубежных моделей [11].

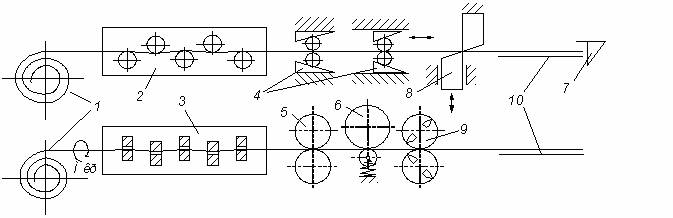
Рис. 1. Схемы правильно-отрезных станков

1 – моток арматурной стали; 2 - роликовый механизм правки; 3 – барабанный механизм правки;

4 – цанговое тянущее устройство; 5 – роликовое тянущее устройство;  6 - мерительный ролик;

7 – конечный выключатель; 8 – ножи (рычажные); 9 – вращающиеся ножи; 10 – приемное устройство.

 

Работа происходит в следующей последовательности. Стержень разматывается из мотка 1 и протягивается через правильное устройство 2 или 3 посредством механизма протягивания 4 или 5, отмеряется на заданную длину мерительным роликом 6 или конечным выключателем 7 и отрезается параллельными (рычажными) ножами 8 или вращающимися ножами 9. Для обеспечения высокой точности отрезки все современные отечественные станки снабжены конечными выключателями 7 и рычажными ножами 8, но в эксплуатации имеется большой парк станков с вращающимися ножами 9, снабженными как мерительным роликом 6, так и конечными выключателями 7, которыми заменили мерительные ролики. На некоторых таких станках вращающиеся ножи заменены рычажными с пневмоприводом.

Роликовые правильные устройства 2 не обеспечивают качественной правки стержней круглого сечения и на современных отечественных правильно-отрезных станках не применяются. В качестве самостоятельных роликовые механизмы применяются в сочетании с машинами для сварки сеток и плоских каркасов, в линиях гибки, а также как на зарубежных, так и на отечественных автоматах для резки коротких стержней. В таких машинах недостаточно качественная правка компенсируется периодической сваркой, дающей шарнир пластичности, или малой длиной заготавливаемого стержня, или пластической деформацией гибки.

Заправка роликовых механизмов правки и регулировка нажимных элементов длительна и выполняется методом «проб и ошибок». На многоточечных машинах для сварки сеток для каждого продольного стержня установлен свой многороликовый механизм правки. Некоторое различие длин стержней в мотках затрудняет одновременность заправки всех продольных стержней.

Высокое качество правки благодаря объемному многократному пластическому изгибу достигается на барабанных механизмах правки 3, применяемых практически почти на всех правильно-отрезных станках в сочетании с роликовыми тянущими устройствами 5 и рычажными ножами 8, что, обеспечивая высокую точность длины отрезаемых стержней, снижает надежность станков. На таких станках на время реза стержень останавливается, а барабан продолжает вращаться. Если барабан имеет 3000 об./мин., а время остановки составляет всего 0,5 с, то за это время под нажимными элементами произойдет 25 знакопеременных изгибов в зонах нажимных элементов в которых, кроме крайних, напряжения будут превышать предел текучести. Этого удается избежать, применив летучие ножницы, сопровождающие движущийся стержень в процессе резки и возвращающиеся в исходное положение. Снижается накопление малоцикловых усталостных явлений на станках, где на время остановки стержня барабану придается возвратно-поступательное движение вдоль его оси [4, 14, 16]. Такие технические решения существенно усложняют конструкцию станков.

Барабанные механизмы правки снабжены нажимными элементами в виде фильер и плашек, что приводит к возникновению сил трения скольжения при протягивании стержня и вращении вокруг него барабана. Это, в свою очередь, приводит к повышенному износу, возрастающему при переходе на правку стержней периодического профиля (при этом наблюдается частичное срезание выступов профиля), а также с повышением прочности обрабатываемых стержней за счет увеличения сил взаимодействия стержня с нажимными элементами. Применение твердосплавных фильер значительно повысило их долговечность, но силы, возникающие в процессе правки, остались прежними, а долговечность остальных узлов станка низкой.

Заправка барабанных механизмов стержнями требует больших физических усилий, особенно при заправке стержнями повышенной прочности и больших диаметров. Время заправки и регулировки эксцентриситетов нажимных элементов опытным станочником составляет 3 – 5 мин. для стержней малых диаметров, 5 – 8 мин. и более для стержней больших диаметров. При правке бухт массой 80 – 100 кг это занимает 10 – 50% рабочего времени. Использование станка улучшается с увеличением массы мотков (поступают мотки массой до 1000 кг). Длительность регулировки механизма правки объясняется неопределенностью износа нажимных элементов. Регулировка выполняется пробным подбором эксцентриситетов нажимных элементов. Как правило, несколько первых стержней каждого мотка имеют кривизну больше допустимой и не могут быть использованы. Увеличение массы мотков уменьшает количество брака, но в процессе правки больших мотков за счет износа фильер или плашек (не твердосплавных) может нарушаться качество правки, и в этом случае необходима остановка станка и дополнительная настройка нажимных элементов барабанного механизма правки.

Основные недостатки могут быть устранены путем совершенствования механизма правки, в котором необходимо сохранить объемный пластический изгиб, но устранить трение скольжения. Это достигается заменой барабанных механизмов правки вибрационными, снабженными роликовыми нажимными элементами. Подвижные секции механизма правки совершают плоскопараллельное движение по круговой траектории и обеспечивают деформацию стержня такого же характера, как в барабанном механизме. При протягивании стержня через вибрационные механизмы правки, трение скольжения заменено трением  качения, что позволяет почти на порядок снизить усилие протягивания. Полностью исключается трение скольжения, имевшее место в барабанных механизмах правки, которое  вызывалось вращением нажимных элементов вокруг стержня (рис. 2) [8]. Использование на правильно-отрезных станках вибрационных механизмов правки вместо барабанных снижает энергоемкость станков или обеспечивает правку стержней больших диаметров и стержней периодического профиля без увеличения мощности станка, при этом исключается имевшее место в барабанных механизмах частичное срезание выступов профиля.

На кафедре строительных и дорожных машин и оборудования (СДМиО) ЛИСИ (ныне кафедра транспортно-технологических машин в строительстве СПбГАСУ) автором разработаны конструкции вибрационных механизмов правки (а.с. №№ 230770, 296708, 365192, 468665, 539640, 732047, 829255, 1139534), [8, 11].

Эксцентриковые механизмы правки с двумя синхронизированными валами являются статически неопределенными системами (а.с. № 230770). Это требует высокой точности при  изготовлении и наладке механизма. Дальнейшая работа на кафедре СДМиО ЛИСИ была направлена на создание статически определимых вибрационных механизмов правки.

Рычажная система вибросекций («прямило» Чебышева) исключает статическую неопределимость  механизма правки и позволяет ограничиться одним эксцентриковым валом, а также вынести в сторону от вала нажимные элементы, что снижает возможность попадания окалины в зону подвижных частей и облегчает заправку стержня. Траектория нажимных элементов близка к окружности (вписывается между двумя концентрическими окружностями с разницей диаметров < 5% и касается их в трех точках) (а.с. № 296708), [8].

Механизм правки с дебалансными вибровозбудителями был спроектирован в КБ треста № 61 «Железобетон» ГЗС и изготовлен в мастерских ЛИСИ для завода ЖБИ в пос. Металлострой (а.с. .№ 468665).

 

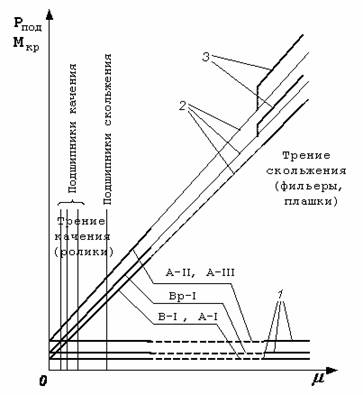
Рис.2. График зависимости силы (Р_под) протягивания стержня и крутящего момента (М_кр) от коэффициента трения μ и профиля арматурной стали

 

Конструктивно проще решается передача движения на вибросекции и синхронизация их движения в механизмах с поводковыми (бегунковыми) вибровозбудителями (а.с. № 539640), в которых, как и в эксцентриковых, имеется два вала, вращающихся синхронно и синфазно, но сечение их значительно меньше, чем в эксцентриковых. В последних важны не только прочность и жесткость эксцентриковых валов, но требуется значительно завышать их диаметр для обеспечения возможности сборки механизма.

На механизмах с поводковыми вибровозбудителями валы передают только крутящий момент, при этом гибкость валов при вращении компенсирует погрешности изготовления механизма. В таких механизмах вибросекции могут быть установлены на упругих опорах с переменной жесткостью и зазором, превышающим амплитуду колебаний вибросекций, что позволяет в процессе правки уравновесить вынуждающую силу и силу изгиба выправляемого стержня. Нагрузка на раму механизма правки или станка от выпрямляемого стержня передается только через неподвижные правильные секции. Опоры подвижных секций переменной жесткости с зазором воспринимают нагрузку от вибросекций только в промежутке времени между окончанием правки и остановкой вибросекции (рис. 3). В процессе правки упругим элементом, воспринимающим нагрузку, является выправляемый стержень (а.с. № 732047) [11].

 

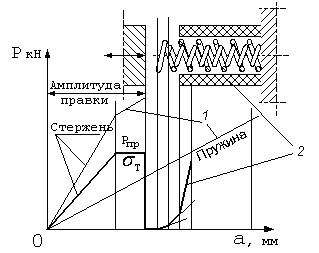
Рис.3. Характеристики опор с учетом упругости выправляемого стержня

1 – пружина; 2 – комбинированная упругая опора с зазором.

 

На механизмах правки с дебалансными, в том числе и с поводковыми вибровозбудителями, регулировка амплитуд вибросекций – прогибов стержней, в зависимости от жесткости последних (EI), частично происходит за счет самонастройки. В таких механизмах с увеличением диаметра обрабатываемых стержней увеличивается сила сопротивления перемещению вибросекций, увеличивается жесткость системы «вибросекции – стержень» и уменьшается амплитуда колебаний, так как возрастает упругая составляющая в шарнире пластичности. Но зависимость между изменением реального прогиба (амплитуды) и требуемым изменением прогиба нелинейная, поэтому необходима регулировка амплитуды за счет изменения массы дебалансов.

Все вышеупомянутые вибрационные механизмы правки, за исключением устройств по а.с. № 296708, могут быть выполнены для одновременной правки нескольких стержней при любом их пространственном расположении (сетки, пространственные каркасы и т.п.). Использование таких механизмов правки, например, в сочетании с АТМС, вместо набора многороликовых механизмов для правки продольных стержней существенно ускоряет настройку механизма правки и этим повышает производительность [8].

Возможно создание станков, обеспечивающих одновременную правку нескольких стержней (нечетное количество), что позволяет более полно использовать установленную мощность и этим существенно повышает производительность. Наиболее эффективно нечетное количество нажимных элементов в каждой секции механизма правки. Например, стержень максимального диаметра обрабатывается один. По мере снижения диаметра можно выправлять 2, 3, 4, 5 стержней. Такие станки наиболее приемлемы для малых, даже мобильных предприятий, например, для строительства коттеджей.

Объединение всех подвижных (четных) секций в единую виброрамку существенно упрощает конструкцию механизма правки (рис. 7, а.с. № 829255), [11] и обеспечивает необходимую для качественной правки эпюру прогибов с минимальными энергозатратами, т.к. такая конструкция выполнена в результате расчета минимально необходимых прогибов выправляемого стержня на нажимных элементах. Дальнейшее снижение энергозатрат достигается возможностью одновременной правки нескольких стержней (рис. 7). Рамка может иметь пары любых по конструкции вибровозбудителей: эксцентриковых, дебалансных, поводковых. Последний механизм внедрен на предприятии п/я Р-6533 (Москва).

Самонастройка требуемой траектории движения выправляемого стержня в зависимости от диаметра на механизме с вибросекциями, установленными на гибких тягах, происходит за счет пружин, натягивающих тяги (а.с. № 1139534). В таком механизма достаточно иметь пару вибровозбудителей только на одной секции, что позволяет получить заданную эпюру прогибов, в т.ч. и «треугольную» (рис. 5), [10].

Попытки выполнить расчеты вибрационных механизмов правки по общепринятой методике [4, 12, 13, 16] показали, что математические модели силы подачи и крутящего момента, принятые в ней дают относительно достоверные результаты для барабанных механизмов правки с нажимными элементами в виде плашек или фильер и дают совершенно неадекватные результаты для других механизмов правки.

 

Общепринятая методика расчета механизмов правки

Анализ зависимостей, разработанных А. С. Квартенко, показал, что они недостаточно полно раскрывают сущность процесса правки, а их полуэмпирический характер позволяет выполнять расчеты только барабанных механизмов правки. В расчетах силы подачи стержня и крутящего момента барабана не учтено перемещение зон деформаций, создаваемых нажимными элементами (рис. 4).

 

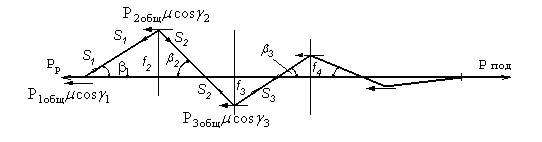
Рис. 4. К определению усилия подачи стержня

 

Из уравнения равновесия сил на первом нажимном элементе получим величину натяжения стержня на первом участке барабана:

;

где Р_р – сила размотки стержня из бухты, Р_δ1 – сопротивление продвижению стержня на первом нажимном элементе, m - приведенный коэффициент трения движения стали по стали (насухо).

Общая нагрузка на первый нажимной элемент правильного барабана составит:

.

Для i-го нажимного элемента правильного барабана получим:

,

где Р_δi – сопротивление продвижению стержня через правильный барабан от изгиба стержня на i-ом нажимном элементе.

.

Сопротивление протягиванию стержня через правильный барабан на i-том нажимном элементе составит:

.

Сопротивление протягиванию стержня через все нажимные элементы правильного барабана составит:

.

Общая сила подачи стержня через правильный барабан составит:

.

Как видно из этих выражений сила сопротивления продвижения стержня через механизм правки учитывает только силу трения.

Аналогичны выражения для расчета крутящего момента:

;
.

Некоторые уточнения и изменения зависимостей по определению сил подачи, крутящего момента барабана и других параметров механизмов правки барабанного типа, также не внесли в математические модели учета перемещения зон деформаций [4, 15, 16].

В беседе автора с А.С. Квартенко по данному вопросу было высказано мнение о том, что необходимо учитывать силу и крутящий момент, затрачиваемые на перемещение зон деформаций, создаваемых нажимными элементами. Возражения А.С. Квартенко сводились к тому, что именно деформации вызывают силу, прижимающую стержень к нажимному элементу; она перпендикулярна оси барабана (на рис. 4 эти силы не показаны) и что дважды одну и ту же силу нельзя учитывать, а также, что для сил перемещения зон деформаций нет реакций на нажимном элементе, а есть только сопротивление трению, вызываемое силой прижатия. Чтобы доказать наличие силы, необходимой для перемещения зон деформаций (шарниров пластичности на 2-ом...(n-1) нажимных элементах), было предложено представить, что m=0; на это А.С. Квартенко возразил, что такого не может быть. Но если согнуть стержень или проволоку (небольшого диаметра) и "перегонять" шарнир пластичности руками, то “внешнее” трение равно нулю, но по теории А. С. Квартенко [12, 13] получается, что сила перемещения "шарнира" пластичности равна нулю, но сила требуется, так как остается внутреннее трение [18], или преодоление сил сопротивления перемещению зоны деформации.  На такой пример А. С. Квартенко возразил, что это другой процесс. Более того, он, вероятно, не обратил внимания на то, что износ плашек и фильер всегда происходит под углом к оси барабана и канавки износа смещены в сторону, обратную направлению вращения. Это позволяет легко обнаружить на нажимном элементе реакции  перемещению и вращению зон деформаций  стержня. Несомненный интерес представляло разобраться в том, учитывается ли металлургами перемещение зон деформаций при расчете правильных машин. Для правки пруткового материала металлурги используют станки Гомельского завода, в расчете механизмов правки которых эта составляющая не учитывалась (станки рассчитывались до появления разработок А.С. Квартенко).

Глубоко рассмотрена теория правки полос и листового материала на многороликовых машинах [20]. При рассмотрении машин, у которых все ролики приводные, принята схема, по которой все силы вертикальны к выправляемой полосе, но смещены от оси роликов, что позволяет рассчитывать их М_кр. В схемах механизмов с приводными роликами одного ряда, а также с неприводными (полоса протягивается или проталкивается) рассматриваются наклонные силы, что, по сути, отражает перемещение зон деформаций. Но в обоих этих случаях принимается, что "для практических расчетов углом наклона и разницей между полным усилием и его вертикальной составляющей можно пренебречь". Для неприводных механизмов правки тянущее усилие (F) определяется по формуле

,

где М_i – изгибающий момент в сечении полосы или листа против i - го ролика; r_ост – радиус остаточной кривизны; D, d – диаметры ролика и цапфы; m – коэффициент трения качения между полосой и роликом; P_i – сила прижатия ролика к полосе.

В этой математической модели учтены силы трения и силы, затрагиваемые на преодоление остаточной кривизны, но не учтены силы на перемещение зон деформаций.

Автору настоящей работы не удалось найти решения этой задачи, ни в теории пластичности, ни в других научных дисциплинах по теории прочности.

 

Учет перемещения зон деформаций в процессе правки

Понимание физической сущности процесса правки и целостное его рассмотрение позволяют составить универсальные обоснованные математические модели для расчета силы подачи и крутящего момента на механизмах правки различных типов, при этом такие модели, даже будучи феноменологическими, объясняют сущность процесса. Такие модели силовых параметров процесса правки будут адекватны реальному процессу правки, если будут учтены все основные составляющие силы подачи стержня и крутящего момента: сила размотки стержня из мотка, трение вертушки с установленным на нем мотком, трение стержня на нажимных элементах и перемещение зон деформаций в процессе правки. Две последние составляющие имеют место как при подаче стержня, так и при вращении механизма правки.

Для нахождения усилия подачи стержня Р_под сначала определяются силы правки P_i из условия обеспечения процесса правки по значениям изгибающих моментов М_т в стержне, вызывающих в зонах нажимных элементов, за исключением крайних, напряжение текучести (рис. 5) [10, 11]. В связи с малой величиной усилия протягивания Р_под по сравнению с усилием растяжения стержня до предела текучести s_т можно принять, что в "шарнирах пластичности" металл находится  на границе упругой зоны и площадки текучести. При определении сил правки Р_i это условие позволяет с достаточной степенью точности воспользоваться зависимостями для упругих деформаций и, рассматривая выправляемый стержень как упругую многопролетную балку, воспринимающую усилия нажимных элементов, определить их значения. Одновременно из-за наличия шарниров пластичности стержень рассматривается как гибкая нить и поэтому углы наклонов сил Р_i не учитываются.

При пластическом изгибе металлического стержня круглого сечения принимается    . В сечении под силой Р_i при данном соотношении W_пл и W_упр имеет место полный шарнир пластичности; по мере удаления от этого сечения зона пластичности уменьшается в сторону крайних волокон [2]. Особенностью процесса правки является то, что при неполном шарнире пластичности возможно равновесие упругих напряжений в центральной зоне сечения и остаточных напряжений, вызванных пластической деформацией (рис. 6) [9]. Неполнота шарнира пластичности учитывается коэффициентом k, который для стержня круглого сечения может колебаться в пределах 0,6…1. После достижения полного шарнира пластичности (k=1) усилие правки Р_i практически не возрастает с увеличением прогибов f_i, а возрастает работа правки.

Силы правки для механизма с пятью нажимными элементами (рис. 5 и 7) составляют:

        (из  );

   (из  );

             (из  );

,               где n – число нажимных элементов.

 Минимально необходимые прогибы, при которых стержень в зонах  нажимных элементов будет находиться на границе упругости и пластичности (текучести), можно определить по формуле Мора, в которой достаточно учесть только М_изг

.

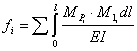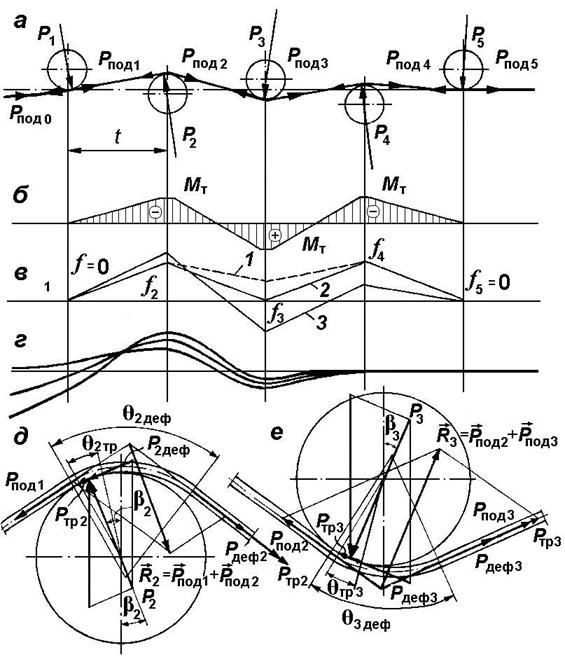
Рис. 5. Силы и деформации во вращающейся плоскости протягивания стержня через пятироликовый механизм правки:

a – траектория движения стержня и силы, действующие на него; б – эпюра изгибающих моментов в стержне; в – эпюры прогибов стержня: 1 – расчетная на минимально необходимые прогибы; 2 – механизма с объединенными в рамку четными нажимными элементами; 3 – рекомендуемая для правки стержней с неопределенной начальной кривизной; г – уменьшение разброса остаточной кривизны по мере прохождения нажимных элементов с f₂ : f₃ : f₄ = 3 : 2 : 1; д, е – схемы сил на втором и третьем нажимных роликах.

 

Для механизмов с пятью нажимными элементами они составят:

а для механизмов с семью и более нажимными элементами будут:

.

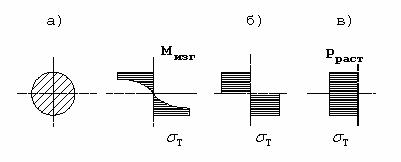
Рис. 6. Напряжение в сечении выпрямленного стержня:

а, б – при изгибе до σ_т; в – при растяжении до σ_т

 

Учесть то, что не только крайние волокна находятся в пластическом состоянии можно введением коэффициентов 1,7 k, что несколько увеличит требуемые расчетные стрелки прогибов, но для их уточнения необходим эксперимент.

Расчетная эпюра 1, видоизмененная на эпюру 2 (рис. 5, в) позволяет при нечетном количестве нажимных элементов объединить четные секции в единую вибрирующую правильную рамку, а нечетные секции оставить неподвижными с f = 0 (рис. 7, а.с. № 829255) [11], что несколько увеличивает углы поворота сечений при изгибе в зонах нажимных элементов.

Усилие подачи стержня при прохождении его через механизм правки нарастает на каждом нажимном элементе. Перед первым нажимным элементом усилие подачи Р_под.0 складывается из силы трения Р_тр.в, определяемой моментом трения М_тр опор вертушки, воспринимаемым стержнем на плече, равном радиусу мотка  r_м, и силы размотки Р_разм, вызываемой пластической деформацией изгиба (М_т = s_т×0,1d³)

.

После прохождения каждого нажимного элемента добавляются сила трения Р_тр.i и сила перемещения зоны деформации по длине стержня Р_деф.i.

;

……………………………

;

…………………………….

,

где в первом приближении без учета угла охвата стержнем нажимного элемента (из-за малой величины этого угла) можно принять, что

,

а Р_{деф i} определена на основании равенства работы А_i, затрачиваемой на перемещение по длине l стержня деформированной зоны, доведенной до полного "шарнира пластичности", с работой, идущей на деформацию растяжения стержня до предела текучести. Такое допущение возможно из-за того, что сечение стержня симметрично относительно нейтральной оси, а диаграммы растяжения и сжатия для стали идентичны, в том числе и при изгибе (кососимметричная эпюра) (рис. 6), поэтому можно принять, что при достижении полного шарнира пластичности  по длине стержня, равной растянутой [9].

,

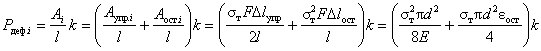где k – эмпирический коэффициент, учитывающий неполноту "шарниров пластичности", а также влияние углов поворота на нажимных элементах (k = 0,6…1); k и e_ост определяются экспериментально.

На барабанных механизмах правки e_ост растяжения мало, и им можно пренебречь, а на вибрационных механизмах с роликовыми нажимными элементами практически не поддается измерению, при изгибе e_ост практически отсутствует из-за многократной смены растяжения сжатием и наоборот, поэтому можно принять

,

где (n – 2) вводится аналогично, как при определении сил на нажимных элементах, пропорционально силам P_i, вызывающим в зонах нажимных элементов деформации как упругие, так и пластические.

Некоторый вклад в величину силы подачи вносит угол q охвата стержнем нажимного элемента, и его влияние из-за малости прогиба и угла q может быть учтено выражением

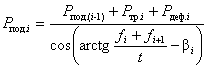
или с помощью зависимости Эйлера

.

Но в этом случае необходимо экспериментально определить: 1) угол q_{i тр}, на котором имеет место внешнее трение (q_{i тр} меньше суммы углов отклонения стержня от оси механизма правки), 2) выяснить возможность использования формулы Эйлера, выведенной для абсолютно гибкой нити, применительно к жесткому стержню, хотя и находящемуся под промежуточными нажимными элементами в состоянии текучести, 3) выяснить значение внешнего коэффициента трения, 4) установить, каким образом должно быть учтено внутреннее трение.

Сравнение расчетных и экспериментальных данных позволит установить, правомерно ли для относительно жесткого стержня разделение сил подачи на каждом нажимном элементе на силу перемещения деформированной зоны и силу трения, вызываемую углом охвата стержня, как это представлено в предыдущем выражении, или жесткость стержня может быть учтена в значениях m и q, тогда зависимость примет вид

.

Выбор зависимости может быть выполнен на основе экспериментальной проверки расчетных значений Р_под.i и Р_под.n по экспериментальным значениям m и q_i.  Значение q_{i деф} для внутреннего трения может быть определено по значениям прогибов f_i на рассматриваемом и соседних нажимных элементах

.

Этот угол учитывает деформации изгиба на участках стержня, не контактирующих с роликом и имеющих место благодаря упругости стержня. Деформацию стержня на каждом нажимном элементе определяет момент пары сил Р_i и R_i (см. рис.5, д, е), который вызывается и уравновешивается изгибающим моментом в стержне, возникающим за счет угла между силами Р_под.(i-1) и Р_под.i  и имеющим место после прохождения зоны контакта стержня с роликом.

В настоящее время при отсутствии этих данных усилие протягивания на любых механизмах правки со значительно более высокой степенью точности по сравнению с методикой [13] может рассчитываться с помощью выражения, учитывающего перемещение зон деформаций, с введением коэффициента k.

 

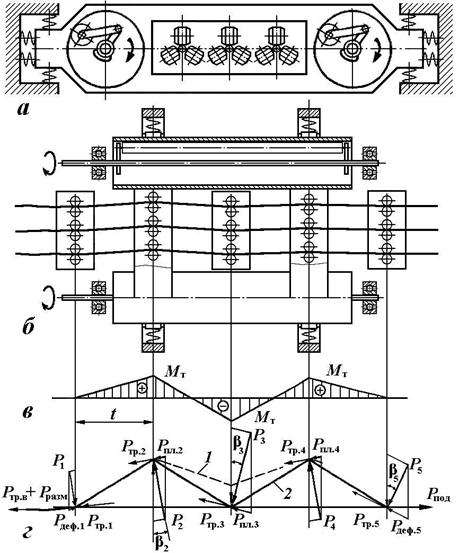
Рис. 7. Вибрационный механизм правки с подвижными секциями,

объединенными в общую рамку

а- схема вибрационной секции; б – схема механизма правки; в -  эпюра моментов;

г – эпюры прогибов: расчетная (1), конструктивная (2)

 

Бóльшая точность достигается при расчете вибрационных механизмов правки с роликовыми  нажимными элементами, имеющими более определенный коэффициент трения качения по сравнению с коэффициентом трения скольжения в барабанном механизме правки, неопределенно изменяющимся в процессе сложного движения, сопровождающегося срезанием со стержня стружки кромками нажимных элементов. Неопределенность коэффициента трения скольжения при расчете по методике [13] дает бóльшую погрешность, чем при расчете вибрационных механизмов правки рассмотренным методом.

Приближенно, без учета углов q_i, усилие подачи стержня может быть определено следующим образом:

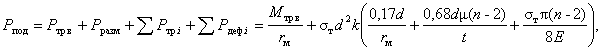
где d – диаметр стержня; s_т  – предел текучести (максимальное значение для данной марки стали); E – модуль упругости обрабатываемой стали; e_ост – остаточное удлинение, возникающее за счет упрочнения крайних  волокон и гистерезиса; М_т – изгибающий момент, создающий шарнир пластичности; r_м – радиус мотка; M_тр.в – момент трения вертушки, учитывающий ее массу с мотком и вид опор вертушки; m – коэффициент трения стержня о нажимные элементы (для барабанных механизмов, где возникает сухое трение скольжения в движении, необходимо учесть, что имеет место резание, оставляющее на поверхности стержня глубокие царапины по винтовой линии и вносящее неопределенность в значение m); n – число нажимных элементов;

t – шаг нажимных элементов; k – коэффициент неполноты шарниров пластичности.

В зоне правки на каждом промежуточном нажимном элементе имеет место следующая взаимосвязь сил: P_i вызывает (), которые дают разность усилий подачи стержня после и до нажимного элемента (), что приводит к отклонению вектора Р_i от вертикального направления к оси механизма правки на угол b_i [11] (см. рис. 5, д, е), сопровождающемуся уводом назад по ходу стержня его контакта с нажимным элементом. Механизм правки за счет крутящегося момента создает силы, нормальные к оси механизма, а за счет перемещения стержня появляется составляющая силы Р_i, направленная вдоль оси стержня в направлении, противоположном его перемещению. Именно эта сила является реакцией на перемещение деформированной зоны вдоль оси стержня. При этом Р_i, P_{i деф} и b_i зависят от механических свойств выправляемого стержня, а b_i также зависит и от величин прогибов на рассматриваемом и соседних нажимных элементах (f_i-1,  f_i,  f_i+1). Такая логическая структура при известных Р_i ,  f_i,  m позволяет методом итераций определить остальные силы взаимодействия выправляемого арматурного стержня и нажимного элемента.

При протягивании стержня наблюдается износ нажимных элементов, на которых имеет место трение скольжения (плашки или фильеры), под углом b₁ к нормали оси правки. Этот угол соответствует углу отклонения Р_i, вызываемого перемещением шарнира прочности (см. рис. 5, 7, 8). Отклонение Р_i от направления, перпендикулярного к оси механизма правки, наблюдается также и на роликовых нажимных элементах. Составляющая силы правки Р_i, направленная вдоль оси стержня, представляет силу сопротивления перемещению шарнира пластичности.

Вращение шарниров пластичности в зонах нажимных элементов также вызывает отклонение силы Р_i от нормали к поверхности нажимного элемента на угол a_i (см. рис. 8). В роликовых нажимных элементах вибрационных механизмов правки отклонение определяется упругим изгибом стержня в плоскости правки. На нажимных элементах, вращающихся вокруг стержня, поворот происходит за счет смещения стержня по поверхности нажимного элемента и упругих сил кручения, вызванных моментами от смещения стержня (М_пл) и трения (М_тр), при этом упругое скручивание и изгиб стержня в плоскости вращения ограничиваются силой трения. На каждом нажимном элементе крутящий момент (М_{i пл}), идущий на вращение шарнира пластичности, (рис. 8) определяется по формуле

.

М_{i тр}, имеющий место только на барабанных механизмах правки, определяется через работу трения (А_{i тр})

.

Суммарный крутящий момент (М_кр) механизма правки

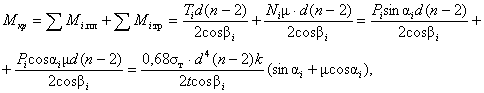
где Т_i и N_i – составляющие сил правки Р_i (см. рис. 8); n – количество нажимных элементов; остальные – см. обозначения в тексте и на рисунках.

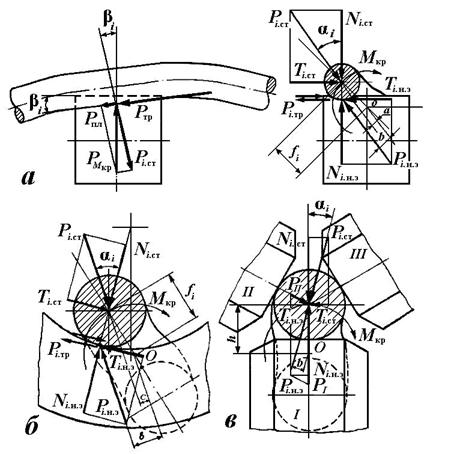
Рис.8. Схемы нажимных элементов и сил, возникающих на плашке (а), в фильере (б) и в трёхроликовом нажимном устройстве (в)

 

В вибрационных механизмах правки с нажимными элементами качения (роликами) М_кр необходим только для вращения шарниров пластичности

.

Угол a_i в начальный момент работы механизма правки возрастает от 0^ºдо определенного значения, средняя величина которого сохраняется в процессе работы. Угол a_i может быть определен на каждом нажимном элементе экспериментально, по смещению канавок на изношенных плашках или фильерах, а также на основании равенства работ вращения шарнира пластичности на один оборот и создания крутящего момента с соответствующей эпюрой напряжения в сечении стержня.

 

Определение динамических характеристик вибрационных механизмов правки

Численное исследование позволило определить шаг нажимных элементов (НЭ) в барабане. Расстояния между НЭ должны соответствовать шагам правки, определяемым формой изгиба стержня и его жесткостью (ЕI) [5].

Теоретические исследования системы нелинейных дифференциальных уравнений, учитывающих соотношения упругих и пластических деформаций в каждом сечении в процессе правки, позволило установить зависимость степени нелинейности от отношения диаметра к шагу нажимных элементов для вибрационного механизма правки [6].

На механизмах правки с дебалансным вибровозбудителем при изменении диаметра обрабатываемого стержня изменяется амплитуда колебаний за счет изменения сил сопротивления стержня изгибу в процессе правки. Суммарная вынуждающая сила дебалансов в каждой секции или правильной рамке, объединяющей четные секции,  ( – суммарный статический момент дебалансов всех вибраторов секции или рамки) затрачивается на преодоление сил инерции колебания секции или рамки, потери в них, на пластические деформации в выправляемом стержне, определяемые коэффициентами демпфирования, и на преодоление упругих сил опор и стержня:

.

В результате решения дифференциального уравнения

определяется вынуждающая сила, учитывающая особенности процесса правки

,

где m_i – масса правильной секции; a_i – амплитуда колебаний; w – угловая частота колебаний (рад/с);  – коэффициент демпфирования секции, учитывающий потери в опорах и на трение стержня (стержней);  – коэффициент демпфирования стержня (стержней), учитывающий затрату сил на пластическую составляющую деформации обрабатываемого стержня (стержней);  – коэффициент жесткости упругих опор;  – коэффициент жесткости выпрямляемого стержня (стержней), учитывающий только упругую составляющую изгиба в процессе правки.

Увеличение амплитуды колебаний  практически не вызывает увеличения усилия как на упругую, так и на пластическую составляющие деформации стержня и только увеличивает энергозатраты за счет большей деформации стержня в зонах шарниров пластичности. Для обеспечения гарантированной правки необходимо, чтобы .

Суммарный статический момент дебалансов каждой подвижной секции выбирается из условия обеспечения максимального усилия правки, т.е. наибольших затрат на деформацию стержня .

С уменьшением диаметра выправляемого стержня сила правки будет уменьшаться и увеличиваться амплитуда колебаний, что необходимо для достижения s_т. При увеличении амплитуды сила будет в большей степени поглощаться инерционной составляющей и упругими опорами . Более точная регулировка амплитуды может производиться заранее, определенным изменением массы дебалансов, а также регулировкой жесткости упругих опор или зазора в опорах с переменной жесткостью и зазором. В последнем случае в процессе правки силы на деформацию упругих опор не потребуется (а.с. № 829255), [1, 3, 11, 17, 19, т.3].

Изменение массы дебалансов компенсирует нелинейность соотношения сил правки и вынуждающих сил дебалансов. Для выявления этой нелинейности рассмотрен конструктивно наиболее простой механизм, в котором подвижные секции объединены в единую рамку (рис. 8), опирающуюся на цилиндрические пружины в двух плоскостях, в каждой из которых установлены взаимно перпендикулярные пружины сжатия.

Решение в виде построения амплитудно-частотной характеристики системы, дающее представление о динамике устройства, найдено с применением метода Рунге-Кутта 4-го порядка [7].

При неопределенности кривизны обрабатываемого стержня наиболее приемлемой, обеспечивающей качество правки будет эпюра прогибов выправляемого стержня, рассмотренная в [13] (см. рис. 5, в, г) и дающая, например, на механизме с пятью нажимными элементами отношение стрелок прогибов и, соответственно, амплитуд колебания подвижных секций

.

Это условие при наличии только двух вибровозбудителей, установленных на одной правильной секции, может быть осуществлено на механизме, в котором все подвижные секции подвешены  на гибких тягах, выполненных, например, в виде стержней, соединенных шарнирно между собой, с подвижными секциями и с основанием, или в виде калиброванных сварных цепей [37].

Решение уравнения движения вибросекций механизма правки на гибких тягах (а.с. № 1138534) позволило найти амплитуды на каждой вибросекции в зависимости от отношения частоты вынужденных колебания к частоте свободных, определяемого силой натяжения пружин тяг, их жесткостью и расположением пары синхронизированных вибровозбудителей на той или иной секции [10].

 

Определение числа оборотов (частоты) механизма правки

Для качественной правки при минимальной затрате энергии необходимо обеспечить оптимальные соотношения числа оборотов и скорости подачи стержня, эксцентриситета и шага нажимных элементов с учетом диаметра и свойств выправляемого стержня. На каждом конкретном механизме заданы шаг нажимных элементов, скорость подачи и число оборотов (на многоскоростном станке – скорости подачи и числа оборотов). Разнообразие механических характеристик и диаметров обрабатываемых стержней затрудняет составление зависимостей параметров механизмов, таких как шаг (t) нажимных элементов, число оборотов (n) барабана (вала вибровозбудителя), эксцентриситет нажимного элемента (f – прогиб изгибаемого стержня). Поэтому используются эмпирические зависимости.

На основе опыта проектирования и эксплуатации станков И.Д. Трофимов (ЦБКМ) предложил формулу для определения скорости вращения правильного барабана (журнал "Кузнечно-штамповочное производство" 1962 г., № 3) [15, 16]

 об/мин,

в которой чем меньше d, тем больше k (k= 5…8).

Оптимальную скорость вращения барабана, при которой остаточный прогиб не превышает 1 мм / пог. м, А.С. Квартенко предложил определять по формуле [4]

 об/мин,

но затем уточнил ее [13]

,

где V_пр – скорость подачи стержня (м/мин), t – шаг нажимных элементов (см), s_т – предел текучести  (кг/см²), Е – модуль упругости (кг/см²), d – диаметр арматурной стали (см).

Ни одна из этих формул не имеет размерности, соответствующей n_бар.

Скорость вращения барабана необходимо выбирать из условия, чтобы в каждой точке поверхности стержня было бы достигнуто s_т, а математическая модель n_бар хоть в какой-то степени отражала бы физическую сущность процесса правки.

Для обеспечения качественной правки шаг (t) нажимных элементов и наименьший диаметр стержней принимаются обычно по наибольшему диаметру обрабатываемого стержня  и  как для роликовых, так и для барабанных механизмов правки [13], а число оборотов барабана принимается . Последняя зависимость не позволяет учитывать диаметр обрабатываемого стержня и соответствует d_min. При правке стержней больших диаметров возможно перекрытие зон пластичности и, соответственно, непроизводительные энергозатраты, которые уменьшаются на многоскоростных станках. Для обоснованного выбора V_пр и n_мех.пр. необходимо учесть жесткость стержня (EI) и изменение его прочностных свойств (s_т/E). Переменный безразмерный коэффициент, уточняющий n_{мех.пр(d)}, можно вывести из зависимостей для определения прогибов стержня под нажимными элементами как многопролетной балки и принять его по второму нажимному элементу

,

где приняты размерности: V (м/мин); s_т и Е (МПа); t, d и f (см). 

 

Литература

1. Бауман В.А., Быховский И.И. Вибрационные машины и процессы в строительстве.– М.: Высш. шк., 1977.– 255 с.

2. Безухов Н. И. Примеры и задачи по теории упругости, пластичности и ползучести. – М.: Высш. шк., 1965.– 320 с.

3. Вибрационные машины в строительстве и производстве строительных материалов: Справ. /Под ред. В. А. Баумана и др. – М.: Машиностроение, 1970. – 548 с.

4. Волков Л. А. Оборудование для производства арматурных железобетонных конструкций.– М.: Машиностроение, 1984.  – 224 с.

5. Волков С. А., Степанов М. М. Влияние формы изгиба арматурного стержня на размещение нажимных элементов в правильном барабане // Повышение эффективности использования машин в строительстве.– Л., 1986.–С.102–112.

6. Волков С. А., Степанов М. А. Выбор шага нажимных элементов  вибрационного устройства для правки арматурных стержней // Повышение эффективности использования машин в строительстве. – Л., 1979. – С. 92 – 98.

7. Волков С. А., Степанов М. М. Методика анализа динамики вибрационных механизмов для правки арматурных стержней // Исследование конструктивных параметров и динамики вибрационных машин. – Ярославль, 1985. – С. 92 – 98.

8.  Волков С. А. Механизмы правки арматурной стали периодического профиля: Нагл. пособие / Ленингр. дом науч.-техн. пропаганды. – Л., 1979. – [12] с.: ил.

9.   Волков С. А., Берталан А. О приближенном расчете усилия протягивания стержней при правке // Строительные и дорожные машины, электротехника, автомобили и двигатели, детали машин: Крат. содерж. докл. к XXVIII науч. конф. ЛИСИ. – Л., 1970. – С. 24 – 27.

10. Волков С. А., Степанов М. М. Определение сил, возникающих в процессе правки арматурных стержней // Повышение эффективности использования машин в строительстве. . – Л., 1984. – С. 113 – 127. и- 27с.

11.  Волков С. А.  Эффективное технологическое оборудование производства арматуры железобетонных конструкций / Ленингр. дом науч.-техн. пропаганды. – Л., 1983.

12.  Картенко А. С. К теории процесса правки стержней арматурной стали на вращающихся барабанах // Исследование землеройных, строительных и дорожных машин. – М., 1966. – С. 133-147.

13. Квартенко А.С. Правильно-отрезные  станки  для  обработки   стержней  арматурной  стали: Обзор. / НИИинформации стройдоркоммунмаш. Сер. 2. Оборудование для  пром. строй. материалов. М., 1965. - 58 с.

14.  Носенко Н. Е. Механизация арматурных работ: Зарубеж. опыт. – 2-е изд. Перераб. и доп. – М.: Стройиздат, 1989. – 223 с.

15.  Носенко Н. Е. Механизация и автоматизация изготовления арматуры для железобетонных конструкций. – М.: Стройиздат, 1970. –352 с.

16.  Носенко Н. Е. Механизация и автоматизация производства  арматурных работ. – 2-е изд. Перераб. и доп. –  М.: Стройиздат, 1982. –223 с.

17.  Пановко Я. Г. Основы прикладной теории колебаний и удара. – 3-е изд., перераб. и доп.– Л.: Машиностроение, Ленингр. отд-ние, 1976. –320 с.

18.  Постников В. С. Внутреннее трение в металлах. – 2-е изд. – М.: Металлургия, 1974. – 250 с.

19.  Прочность. Устойчивость. Колебания: Справочник в 3-х т./ Под общ. ред. И. А. Биргера и Я. Г. Пановко. – М.: Машиностроение.

         Т.1, 1968. –831 с.

         Т.2, 1968. –463 с.

         Т.3, 1968. – 567 с.

20.  Слоним А. З., Сонин А. Л. Правка листового и сортового металла. – М.: Металлургия, 1981. – 232 с.

  

Опубликовано в монографии: ФИЗИЧЕСКИЕ ОСНОВЫ РАБОЧИХ ПРОЦЕССОВ МАШИН ДЛЯ ИЗГОТОВЛЕНИЯ АРМАТУРЫ ЖЕЛЕЗОБЕТОННЫ КОНСТРУКЦИЙ. / С. А. Волков; С. – Петерб. гос. архитектур. – строит. ун-т. – СПб. – 2001. – 125 с.